
【题目】以平面直角坐标系![]() 的原点为极点,
的原点为极点,![]() 轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的长度单位,直线
轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的长度单位,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 是参数),圆
是参数),圆![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求直线![]() 的普通方程与圆
的普通方程与圆![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设曲线![]() 与直线
与直线![]() 的交于
的交于![]() ,
,![]() 两点,若
两点,若![]() 点的直角坐标为
点的直角坐标为![]() ,求
,求![]() 的值.
的值.
 走进文言文系列答案
走进文言文系列答案科目:高中数学 来源: 题型:
【题目】判断下列命题的真假.
(1)如果直线![]() 平行于直线
平行于直线![]() ,则
,则![]() 平行于经过
平行于经过![]() 的任何一个平面;
的任何一个平面;
(2)如果一条直线不在平面内,则这条直线就与这个平面平行;
(3)过直线外一点,可以作无数个平面与这条直线平行;
(4)如果一条直线与一个平面平行,则它与该平面内的任何直线都平行.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我校为了解学生喜欢通用技术课程“机器人制作”是否与学生性别有关,采用简单随机抽样的办法在我校高一年级抽出一个有60人的班级进行问卷调查,得到如下的![]() 列联表:
列联表:
喜欢 | 不喜欢 | 合计 | |
男生 | 18 | ||
女生 | 6 | ||
合计 | 60 |
已知从该班随机抽取1人为喜欢的概率是![]() .
.
(Ⅰ)请完成上面的![]() 列联表;
列联表;
(Ⅱ)根据列联表的数据,若按90%的可靠性要求,能否认为“喜欢与否和学生性别有关”?请说明理由.
参考临界值表:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式:![]() 其中
其中![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某研究性学习小组为了调查研究学生玩手机对学习的影响,现抽取了30名学生,得到数据如表:
玩手机 | 不玩手机 | 合计 | |
学习成绩优秀 | 8 | ||
学习成绩不优秀 | 16 | ||
合计 | 30 |
已知在全部的30人中随机抽取1人,抽到不玩手机的概率为![]() .
.
(1)请将2×2列联表补充完整;
(2)能否在犯错误的概率不超过0.005的前提下认为玩手机对学习有影响;
(3)现从不玩手机,学习成绩优秀的8名学生中任意选取两人,对他们的学习情况进行全程跟踪,记甲、乙两名学生被抽到的人数为X,求X的分布列和数学期望.
附:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了落实国务院“提速降费”的要求,某市移动公司欲下调移动用户消费资费.已知该公司共有移动用户10万人,人均月消费50元.经测算,若人均月消费下降x%,则用户人数会增加![]() 万人.
万人.
(1)若要保证该公司月总收入不减少,试求x的取值范围;
(2)为了布局“5G网络”,该公司拟定投入资金进行5G网络基站建设,投入资金方式为每位用户月消费中固定划出2元进入基站建设资金,若使该公司总盈利最大,试求x的值.
(总盈利资金=总收入资金-总投入资金)
查看答案和解析>>
科目:高中数学 来源: 题型:
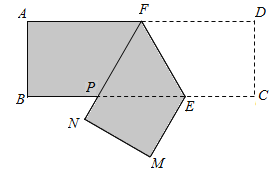
【题目】如图,某机械厂要将长![]() ,宽
,宽![]() 的长方形铁皮
的长方形铁皮![]() 进行裁剪.已知点
进行裁剪.已知点![]() 为
为![]() 的中点,点
的中点,点![]() 在边
在边![]() 上,裁剪时先将四边形
上,裁剪时先将四边形![]() 沿直线
沿直线![]() 翻折到
翻折到![]() 处(点
处(点![]() ,
,![]() 分别落在直线
分别落在直线![]() 下方点
下方点![]() ,
,![]() 处,
处,![]() 交边
交边![]() 于点
于点![]() ,再沿直线
,再沿直线![]() 裁剪.
裁剪.
(1)当![]() 时,试判断四边形
时,试判断四边形![]() 的形状,并求其面积;
的形状,并求其面积;
(2)若使裁剪得到的四边形![]() 面积最大,请给出裁剪方案,并说明理由.
面积最大,请给出裁剪方案,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com