Question

12．碧波万顷的大海上，“蓝天号”渔轮在A处进行海上作业，“白云号”货轮在“蓝天号”正南方向距“蓝天号”20nmile的B处．现在“白云号”以每小时10nmile的速度向正北方向行驶，而“蓝天号”同时以每小时8nmile的速度由A处向南偏西60°方向行驶，经过$\frac{70}{61}$小时后，“蓝天号”和“白云号“两船相距最近．

Answer 1

分析 利用余弦定理求出两船的距离关于时间t的函数，求出该函数取得最小值时对于的t即可．

解答 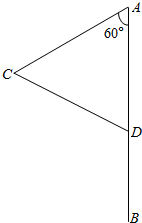解：设经过t小时后蓝天号渔船航行至C处，白云号货轮航行至D处，则AC=8t，AD=20-10t，∠A=60°．0＜t＜2．
在△ACD中，由余弦定理得CD²=AC²+AD²-2AC•AD•cosA．
∴CD²=64t²+（20-10t）²-8t（20-10t）=244t²-560t+400．
∴当t=$\frac{560}{488}$=$\frac{70}{61}$时，CD²取得最小值，即“蓝天号”和“白云号“两船相距最近．
故答案为$\frac{70}{61}$．

点评 本题考查了余弦定理在解三角形中的应用，二次函数的最值，属于中档题．