
| 女性用户 | 分值区间 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100) |
| 频数 | 20 | 40 | 80 | 50 | 10 | |
| 男性用户 | 分值区间 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100) |
| 频数 | 45 | 75 | 90 | 60 | 30 |
分析 (Ⅰ)作出女性用户和男性用户的频率分布直方图,由图可得女性用户的波动小,男性用户的波动大.
(Ⅱ)运用分层抽样从男性用户中抽取20名用户,评分不低于80分有6人,其中评分小于90分的人数为4,记为A,B,C,D,评分不小于90分分的人数为2,记为a,b,从6人人任取2人,利用列举法能求出两名用户评分都小于90分的概率.
解答 解:(Ⅰ)女性用户和男性用户的频率分布直方图分别如下左、右图: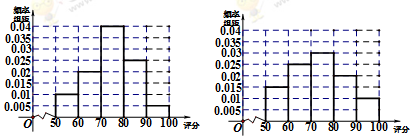
由图可得女性用户的波动小,男性用户的波动大.
(Ⅱ)运用分层抽样从男性用户中抽取20名用户,评分不低于80分有6人,
其中评分小于90分的人数为4,记为A,B,C,D,
评分不小于90分分的人数为2,记为a,b,从6人人任取2人,
基本事件空间为:
Ω={(AB),(AC),(AD),(Aa),(Ab),(BC),(BD),(Ba),(Bb),(CD),(Ca),(Cb),(Da),(Db),(ab)},共有15个元素.
其中把“两名用户评分都小于90分”记作M,
则M={(AB),(AC),(AD),(BC),(BD),(CD)},共有6个元素.
所以两名用户评分都小于90分的概率为p=$\frac{6}{15}=\frac{2}{5}$.
点评 本题考查频率分布直方图的应用,考查概率的求法,是基础题,解题时要认真审题,注意列举法的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x>3} | B. | {x|x>1} | C. | {x|-1<x<3} | D. | {x|1<x<3} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
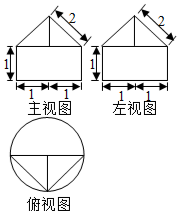 一个几何体的三视图如图所示,则该几何体的体积为( )
一个几何体的三视图如图所示,则该几何体的体积为( )| A. | 2π+$\frac{\sqrt{3}}{3}$ | B. | π+$\frac{\sqrt{3}}{3}$ | C. | 2π+$\frac{\sqrt{3}}{3}$ | D. | π+$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | M=P | B. | P≠M | C. | N∩P≠∅ | D. | M∩N≠∅ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com