Question

13．一个圆锥的底面半径为2cm，高为6cm，其中有一个高为xcm的内接圆柱．
（1）求圆锥的侧面积；
（2）当x为何值时，圆柱的侧面积最大？并求出最大值．

Answer 1

分析 （1）求出圆锥的母线长，利用侧面积公式求解即可．
（2）由（1）由题意作出几何体的轴截面，根据轴截面和比例关系列出方程，求出圆柱的底面半径，再表示出圆柱的侧面积；根据基本不等式求出侧面面积的最大值．

解答 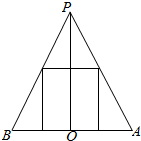解：（1）母线长为：$\sqrt{{6}^{2}+{2}^{2}}$=$2\sqrt{10}$（cm），所以圆锥的侧面积S=πrl=4$\sqrt{10}π$．（cm²）．
（2）设所求的圆柱的底面半径为r，它的轴截面如图：
由图得，$\frac{r}{2}$=$\frac{6-x}{6}$，即r=2-$\frac{x}{3}$．
∴S_圆柱侧=2πrx=2π（2-$\frac{x}{3}$）x=4πx-$\frac{2π}{3}$x2≤$\frac{2}{3}[\frac{（6-x）+x}{2}]^{2}π$=6π
当且仅当x=3时取等号，∴当圆柱的高为3cm时，它的侧面积最大为6πcm²（10分）．

点评 本题的考点是简单组合体的面积问题，关键是作出轴截面，求出长度之间的关系式，表示出面积后利用函数的思想求出最值，考查了数形结合思想和函数思想．