
 春节期间,某校高二学生随交警对某高速公路某路段上行驶的七座以下小型汽车进行监控抽查,抽查方式按进入该路段的先后梅间隔20辆就抽取一辆的方法进行,共抽取了40辆,将它们的车速(km/h)分成6段区间:(70,80],(80,90],(90,100],(100,110],(110,120],(120,130],后得到如图的频率分布直方图.已知该段高速公路的规定时速为100km/h,超过规定时速将被罚款,规定如下:超过规定时速10%以内(含),不罚款;超过规定时速10%以上未超过20%的,处以50元罚款;超过规定时速20%以上未超过50%的,处以200元罚款.
春节期间,某校高二学生随交警对某高速公路某路段上行驶的七座以下小型汽车进行监控抽查,抽查方式按进入该路段的先后梅间隔20辆就抽取一辆的方法进行,共抽取了40辆,将它们的车速(km/h)分成6段区间:(70,80],(80,90],(90,100],(100,110],(110,120],(120,130],后得到如图的频率分布直方图.已知该段高速公路的规定时速为100km/h,超过规定时速将被罚款,规定如下:超过规定时速10%以内(含),不罚款;超过规定时速10%以上未超过20%的,处以50元罚款;超过规定时速20%以上未超过50%的,处以200元罚款.分析 (1)根据抽样方法的特征,判断是系统抽样,根据频率分布直方图,求出样本数据的众数和中位数的估计值求出中位数落在的区间;
(2)直接利用平均数就是公式求解即可.
(3)受到罚款的车辆共6辆,从6辆小型汽车中任取2辆共有15种取法,然后求解该学生所得学业赞助费超过200元的概率.
解答 解:(1)监控抽查采取的是系统抽样方法…(1分)
∵频率分布直方图中a=0.1-(0.005+0.01×3+0.025)=0.04
∴6段区间的人数依次是4,10,16,4,4,2人
故中位数落在(90,100]内…(3分)
(2)这40辆小型汽车的平均车速为$\frac{4×75+10×85+16×95+4×105+4×115+2×125}{40}=95$(km/h)…(6分)
(3)受到罚款的车辆共6辆,从6辆小型汽车中任取2辆共有15种取法…(8分)
罚款总金额超过200元的情形有9种…(10分)
故该学生所得学业赞助费超过200元的概率为$P=\frac{9}{15}=\frac{3}{5}$…(12分)
点评 本题考查均值的求法,考查离频率分布直方图的应用,古典概型概率的求法,解题时要认真审题.


科目:高中数学 来源: 题型:解答题
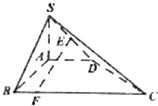 在四棱锥S-ABCD中,SA⊥平面ABCD,∠BAD=∠ABC=90°,SA=AB=AD=$\frac{1}{3}$BC=1,E为SD的中点.
在四棱锥S-ABCD中,SA⊥平面ABCD,∠BAD=∠ABC=90°,SA=AB=AD=$\frac{1}{3}$BC=1,E为SD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,2] | B. | ∅ | C. | [-4,-1] | D. | [-4,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,$\frac{4}{3}$) | B. | ($\frac{1}{2}$,$\frac{4}{3}$) | C. | (1,$\frac{7}{4}$) | D. | ($\frac{1}{2}$,$\frac{7}{4}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com