
 如图,设锐角△ABC的外接圆ω的圆心为O,经过A,O,C三点的圆ω1的圆心为K,且与边AB和BC分别相交于点M和N,现知点L与K关于直线MN对称,证明:BL⊥AC.
如图,设锐角△ABC的外接圆ω的圆心为O,经过A,O,C三点的圆ω1的圆心为K,且与边AB和BC分别相交于点M和N,现知点L与K关于直线MN对称,证明:BL⊥AC. 分析 连接OB,LK,OK,AN,取BC的中点D,连接OD,运用同弧(等弧)所对的圆周角和圆心角的关系,BO⊥MN,由对称性可得BO∥LK;运用三角形全等的判定可得△AOK≌△LKM,得出LK=OA=OB,得出四边形BLKO为平行四边形,即可得证.
解答 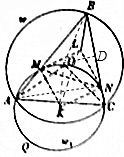 证明:如图,连接OB,LK,OK,AN,取BC的中点D,连接OD,
证明:如图,连接OB,LK,OK,AN,取BC的中点D,连接OD,
由∠OBN+∠BNM=∠OBN+∠BAC=∠OBN+∠BOD=90°,
得出BO⊥MN,又LK⊥MN,故BO∥LK…①
又∠BAN=∠BAO+∠OAN=∠BAO+∠OCB=∠ABO+∠CBO=∠ABC,
而2∠BAN=2∠BAC+2∠CAN=2∠MNC+2∠CAN=∠MKC+∠CKN=∠MKN,
且2∠ABC=∠AOC,故∠MKN=∠AOC,
因此∠AOK=∠MKL,又KO=KA=KM=ML,
于是∠OAK=∠AOK=∠MKL=∠MLK,
所以△AOK≌△LKM,因此得出LK=OA=OB…②
由①②得出四边形BLKO为平行四边形,
故BL∥OK,由OK⊥AC,
因此有BL⊥AC.
点评 本题考查圆的垂径定理、同弧(等弧)所对的圆周角和圆心角的关系、全等三角形的判定和性质和两直线平行的判定和性质,考查推理和运算能力,属于难题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | (a2+a3-a1,b2+b3-b1) | B. | (b2+b3-b1,a2+a3-a1) | ||
| C. | (a2+a3-2a1,b2+b3-2b1) | D. | (b2+b3-2b1,a2+a3-2a1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
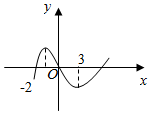 已知函数f(x)=x3+bx2+cx+d的图象如图,则函数y=lnf′(x)的单调减区间为( )
已知函数f(x)=x3+bx2+cx+d的图象如图,则函数y=lnf′(x)的单调减区间为( )| A. | [0,3) | B. | [-2,3] | C. | (-∞,-2) | D. | [3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com