
| A. | 2016 | B. | 2017 | C. | log22017 | D. | $\frac{2017}{2}$ |
分析 由已知得an=2${\;}^{{b}_{n}}$,计算$\frac{{a}_{n+1}}{{a}_{n}}$可判断{an}为等比数列,于是a1a2017=a9a2009=4,从而得出b1+b2017=2,代入等差数列的求和公式即可.
解答 解:设{bn}的公差为d,
∵bn=log2an,∴an=2${\;}^{{b}_{n}}$,
∴$\frac{{a}_{n+1}}{{a}_{n}}$=$\frac{{2}^{{b}_{n+1}}}{{2}^{{b}_{n}}}$=2${\;}^{{b}_{n+1}-{b}_{n}}$=2d.
∴{an}是等比数列,
∴a1a2017=a9a2009=4,
即2${\;}^{{b}_{1}}$•2${\;}^{{b}_{2017}}$=2${\;}^{{b}_{1}+{b}_{2017}}$=4,
∴b1+b2017=2,
∴b1+b2+b3+…+b2017=$\frac{{b}_{1}+{b}_{2017}}{2}×2017$=2017.
故选B.
点评 本题考查了等差数列,等比数列的性质,前n项和公式,属于中档题.


科目:高中数学 来源: 题型:解答题
| 单价x(元) | 18 | 19 | 20 | 21 | 22 |
| 销量y(册) | 61 | 56 | 50 | 48 | 45 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{3}{2}$ | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0.1,0.2,0.3) | B. | (0,0,0.001) | C. | (5,0,0) | D. | (0,0.01,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ${4^{0.2}}<{3^{0.4}}<{log_{0.4}}0.5<{3^{0.5}}$ | B. | ${log_{0.4}}0.5<{3^{0.4}}<{4^{0.2}}<{3^{0.5}}$ | ||
| C. | ${log_{0.4}}0.5<{3^{0.5}}<{4^{0.2}}<{3^{0.4}}$ | D. | ${log_{0.4}}0.5<{4^{0.2}}<{3^{0.4}}<{3^{0.5}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
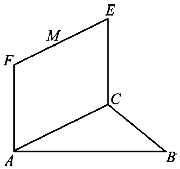 如图,矩形ACEF和等边三角形ABC中,AC=2,CE=1,平面ABC⊥平面ACEF.
如图,矩形ACEF和等边三角形ABC中,AC=2,CE=1,平面ABC⊥平面ACEF.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
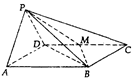 如图,在四棱锥中P-ABCD中,底面ABCD是菱形,且∠DAB=60°,PA=PD,M为CD的中点,平面PAD⊥平面ABCD.
如图,在四棱锥中P-ABCD中,底面ABCD是菱形,且∠DAB=60°,PA=PD,M为CD的中点,平面PAD⊥平面ABCD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com