
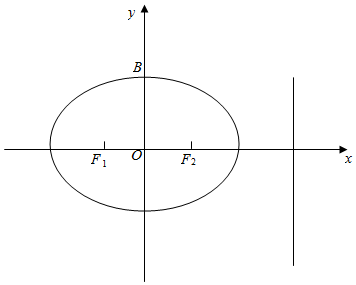
 ��ͼ����ƽ��ֱ������ϵxOy�У���ԲE��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0����������Ϊ$\frac{1}{2}$����B��0��$\sqrt{3}$������ԲE���϶��㣬F1��F2�ֱ�����ԲE�����ҽ��㣮
��ͼ����ƽ��ֱ������ϵxOy�У���ԲE��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0����������Ϊ$\frac{1}{2}$����B��0��$\sqrt{3}$������ԲE���϶��㣬F1��F2�ֱ�����ԲE�����ҽ��㣮���� ��1����e=$\frac{1}{2}=\frac{c}{a}$��b=$\sqrt{3}$��a2=b2+c2������������ɵó���
��2������Բ�ĵڶ������֪��|MF1|=$\frac{1}{2}{x}_{0}$+2����M�����ߵľ���d=4-x0�����ݣ��Ե�MΪԲ�ģ�MF1Ϊ�뾶��Բ����ԲE�������й����㣬�ɵ�|MF1|��d���õ�x0����Сֵ�����ɵõ�|y0|�����ֵ���ɵá�F1MF2��������ֵS=$\frac{1}{2}��2c��|{y}_{0}{|}_{max}$��
��3����ֱ��BP��BQ��ֱ�߷��̷ֱ�Ϊ��y=kx+$\sqrt{3}$��y=-$\frac{1}{k}$x+$\sqrt{3}$���ֱ�����Բ���������ɵõ�P��Q�����꣬���õ�бʽ���ɵó���
��� �⣺��1����e=$\frac{1}{2}=\frac{c}{a}$��b=$\sqrt{3}$��a2=b2+c2��������ã�c=1��a=2��b=$\sqrt{3}$��
����ԲE�ķ���Ϊ$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}$=1��
��2����Բ�������߷ֱ�Ϊ��x=-4��x=4��F1��-1��0������M��x0��y0����
����Բ�ĵڶ������֪��$\frac{|M{F}_{1}|}{{x}_{0}-��-4��}=\frac{1}{2}$����Ϊ��$\frac{1}{2}{x}_{0}$+2��
��M�����ߵľ���d=4-x0��
���Ե�MΪԲ�ģ�MF1Ϊ�뾶��Բ����ԲE�������й����㣬
��|MF1|��d��
��$\frac{1}{2}{x}_{0}$+2��4-x0�����2��${x}_{0}��\frac{4}{3}$��
��${y}_{0}^{2}$=3$��1-\frac{{x}_{0}^{2}}{4}��$��$3��[1-\frac{1}{4}����\frac{4}{3}��^{2}]$=$\frac{5}{3}$��
ȡ|y0|�����ֵ$\sqrt{\frac{5}{3}}$��
���F1MF2��������ֵS=$\frac{1}{2}��2c��|{y}_{0}{|}_{max}$=1��$\sqrt{\frac{5}{3}}$=$\frac{\sqrt{15}}{3}$��
��3��֤������ֱ��BP��BQ��ֱ�߷��̷ֱ�Ϊ��y=kx+$\sqrt{3}$��y=-$\frac{1}{k}$x+$\sqrt{3}$��
����$\left\{\begin{array}{l}{y=kx+\sqrt{3}}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$����Ϊ����3+4k2��x2+8$\sqrt{3}$kx=0���ɵ�xP=-$\frac{8\sqrt{3}k}{3+4{k}^{2}}$��yP=$\frac{-4\sqrt{3}{k}^{2}+3\sqrt{3}}{3+4{k}^{2}}$��
����$\left\{\begin{array}{l}{y=-\frac{1}{k}x+\sqrt{3}}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$���ɵã�xQ=$\frac{8\sqrt{3}k}{3{k}^{2}+4}$��yQ=$\frac{3\sqrt{3}{k}^{2}-4\sqrt{3}}{3{k}^{2}+4}$��
��ֱ��PQ�ķ���Ϊ��y-$\frac{3\sqrt{3}{k}^{2}-4\sqrt{3}}{3{k}^{2}+4}$=$\frac{3��{k}^{2}-1��}{7k}$$��x-\frac{8\sqrt{3}k}{3{k}^{2}+4}��$��
��x=0���ɵ�y=$-\frac{\sqrt{3}}{7}$��
��ֱ��PQ�ؾ���y���ϵ�һ������$��0��-\frac{\sqrt{3}}{7}��$��
���� ���⿼������Բ�ı����̼������ʡ�ֱ������Բ�ཻ���⡢���ֱ��ֱ��б��֮��Ĺ�ϵ����������������������������������⣮


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{7}{32}$ | B�� | $\frac{7\sqrt{3}}{32}$ | C�� | $\frac{7}{16}$ | D�� | $\frac{7\sqrt{3}}{16}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com