
分析 (1)求出函数的导数,计算f(1),f′(1)的值,求出切线方程即可;
(2)求出函数的导数,通过讨论t的范围求出函数的单调区间,从而求出f(x)的最小值即可;
(3)设m(x)=$\frac{x}{{e}^{x}}$-$\frac{2}{e}$,(x∈(0,+∞)),求出m(x)的导数,求出m(x)的最大值,得到f(x)min≥-$\frac{1}{e}$≥m(x)max恒成立,从而证明结论即可.
解答 解:(1)f′(x)=lnx+x•$\frac{1}{x}$=lnx+1,
x=1时,f′(1)=1,f(1)=0,
故f(x)在x=1处的切线方程是:y=x-1,
联立$\left\{\begin{array}{l}{y=x-1}\\{y={-x}^{2}+ax-2}\end{array}\right.$,
消去y得:x2+(1-a)x+1=0,
由题意得:△=(1-a)2-4=0,
解得:a=3或-1;
(2)由(1)得:f′(x)=lnx+1,
x∈(0,$\frac{1}{e}$)时,f′(x)<0,f(x)递减,
x∈($\frac{1}{e}$,+∞)时,f′(x)>0,f(x)递增,
①0<t<t+$\frac{1}{4}$≤$\frac{1}{e}$,即0<t≤$\frac{1}{e}$-$\frac{1}{4}$时,
f(x)min=f(t+$\frac{1}{4}$)=(t+$\frac{1}{4}$)ln(t+$\frac{1}{4}$),
②0<t<$\frac{1}{e}$<t+$\frac{1}{4}$,即$\frac{1}{e}$-$\frac{1}{4}$<t<$\frac{1}{e}$时,
f(x)min=f($\frac{1}{e}$)=-$\frac{1}{e}$;
③$\frac{1}{e}$≤t<t+$\frac{1}{4}$,即t≥$\frac{1}{e}$时,f(x)在[t,t+$\frac{1}{4}$]递增,
f(x)min=f(t)=tlnt;
综上,f(x)min=$\left\{\begin{array}{l}{(t+\frac{1}{4})ln(t+\frac{1}{4}),0<t≤\frac{1}{e}-\frac{1}{4}}\\{-\frac{1}{e},\frac{1}{e}-\frac{1}{4}<t<\frac{1}{e}}\\{tlnt,t≥\frac{1}{e}}\end{array}\right.$;
(3)证明:设m(x)=$\frac{x}{{e}^{x}}$-$\frac{2}{e}$,(x∈(0,+∞)),则m′(x)=$\frac{1-x}{{e}^{x}}$,
x∈(0,1)时,m′(x)>0,m(x)递增,
x∈(1,+∞)时,m′(x)<0,m(x)递减,
可得m(x)max=m(1)=-$\frac{1}{e}$,当且仅当x=1时取到,
由(2)得f(x)=xlnx,(x∈(0,+∞))的最小值是-$\frac{1}{e}$,
当且仅当x=$\frac{1}{e}$时取到,
因此x∈(0,+∞)时,f(x)min≥-$\frac{1}{e}$≥m(x)max恒成立,
又两次最值不能同时取到,
故对任意x∈(0,+∞),都有$xlnx>\frac{x}{e^x}-\frac{2}{e}$成立.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及分类讨论思想、转化思想,是一道综合题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | b>a>c | C. | b>c>a | D. | c>b>a |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π),其导函数的图象f'(x)如图所示,则$f({\frac{π}{2}})$的值为( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π),其导函数的图象f'(x)如图所示,则$f({\frac{π}{2}})$的值为( )| A. | $2\sqrt{3}$ | B. | 2 | C. | $2\sqrt{2}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
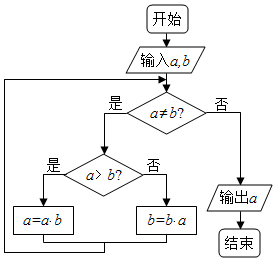 如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入a,b分别为2,8,则输出的a等于( )
如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入a,b分别为2,8,则输出的a等于( )| A. | 4 | B. | 0 | C. | 14 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com