考点:利用导数研究函数的极值,利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:(Ⅰ)令f′(x)=e
x-1=0,得x=1,由此利用导数性质能求出f(x)的单调区间与极值.
(Ⅱ)g′(x)=acosx,g′(
)=
a=,由此利用导数的性质能求出g(x)=sinx+1.
(Ⅲ)当x≥0时,sinx+1≤me
x,令h(x)=sinx+1-me
x,由此利用分类讨论思想和导数性质能求出实数的取值范围.
解答:
解:(Ⅰ)令f′(x)=e
x-1=0,得x=0,(1分)
∴当x>0时,f′(x)>0;当x<0时,f′(x)<0.
∴f(x)的增区间为(-∞,0),减区间为(0,+∞),
∴f(x)
极小值=f(0)=1.(3分)
(Ⅱ)g′(x)=acosx,g′(
)=
a=,解得a=1.
又g(
)=
+b,
∴6
•-12(
+b)+18-
π=0,∴b=1,
∴g(x)=sinx+1.( 6分)
(Ⅲ)当x≥0时,sinx+1≤me
x,令h(x)=sinx+1-me
x,
当m<1时,h(0)=1-m>0矛盾,( 8分)
首先证明sinx≤x在[0,+∞)恒成立.
令r(x)=sinx-x,r′(x)=cosx-1≤0,
故r(x)为[0,+∞)上的减函数,
r(x)≤r(0)=0,故sinx≤x,(10分)
由(Ⅰ)知e
x≥x+1,故当m≥1时,
h(x)=sinx+1-me
x≤e
x-me
x=e
x-me
x=(1-m)e
x≤0,
综上m≥1.(12分)
点评:本题重点考查利用导数研究函数的性质,利用函数的性质解决不等式、方程问题.重点考查学生的代数推理论证能力,解题时要认真审题,注意导数性质的合理运用.



 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案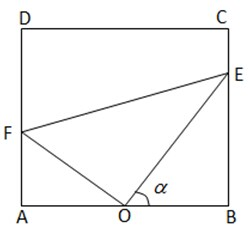 南海中学校园内建有一块矩形草坪ABCD,AB=50米,BC=25
南海中学校园内建有一块矩形草坪ABCD,AB=50米,BC=25