
分析 (1)利用向量的坐标求解所求向量的坐标,利用数量积运算法则求解即可.
(2)利用数量积求解向量的夹角即可.
解答 解:(1)向量$\overrightarrow{a}$=(-2,1),$\overrightarrow{b}$=(3,-4).
($\overrightarrow{a}$+$\overrightarrow{b}$)=(1,-3),(2$\overrightarrow{a}$-$\overrightarrow{b}$)=(-7,6).
所以($\overrightarrow{a}$+$\overrightarrow{b}$)•(2$\overrightarrow{a}$-$\overrightarrow{b}$)=-7-18=-25.
(2)$\overrightarrow{a}$+$\overrightarrow{b}$=(1,-3),
cos<$\overrightarrow{a}$,$\overrightarrow{a}$+$\overrightarrow{b}$>=$\frac{\overrightarrow{a}•(\overrightarrow{a}+\overrightarrow{b})}{|\overrightarrow{a}||\overrightarrow{a}+\overrightarrow{b}|}$=$\frac{-5}{\sqrt{5}×\sqrt{1+9}}$=-$\frac{\sqrt{2}}{2}$.
向量$\overrightarrow{a}$与$\overrightarrow{a}$+$\overrightarrow{b}$的夹角为135°.
点评 本题考查向量的数量积的运算,考查计算能力.


 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在直三棱柱ABC-A1B1C1中,AB⊥AC,D,E分别为AB,BC的中点,点F在侧棱BB1上,且A1F⊥B1D,求证:
如图,在直三棱柱ABC-A1B1C1中,AB⊥AC,D,E分别为AB,BC的中点,点F在侧棱BB1上,且A1F⊥B1D,求证:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,椭圆E的左、右焦点分别为F1,F2,过F1且斜率为$\frac{4}{3}$的直线交椭圆E于P,Q两点,若△PF1F2为直角三角形,则椭圆E的离心率为$\frac{1}{3}$或$\frac{5}{7}$.
如图,椭圆E的左、右焦点分别为F1,F2,过F1且斜率为$\frac{4}{3}$的直线交椭圆E于P,Q两点,若△PF1F2为直角三角形,则椭圆E的离心率为$\frac{1}{3}$或$\frac{5}{7}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
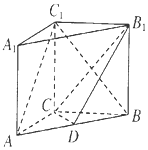 如图,在直三棱柱ABC-A1B1C1中,三角形ABC为等腰直角三角形,AC=BC=$\sqrt{2}$,AA1=1,点D是AB的中点.
如图,在直三棱柱ABC-A1B1C1中,三角形ABC为等腰直角三角形,AC=BC=$\sqrt{2}$,AA1=1,点D是AB的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com