
分析 (1)计算所有事件数已经满足条件的事件数,利用古典概型公式求之;
(2)设两人到达的时间分别为9点到10点之间的x分钟、y分钟.用(x,y)表示每次试验的结果,分别,x,y范围表示满足条件的事件,利用几何概型的概率公式得到所求.
解答 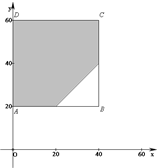 解:(1)从袋中6个球中无放回的摸出2个,试验的结果共有6×5=30种,中奖的情况分为两种:
解:(1)从袋中6个球中无放回的摸出2个,试验的结果共有6×5=30种,中奖的情况分为两种:
(i)2个球都是红色,包含的基本事件数为2×1=2;
(ii)2个球都是白色,包含的基本事件数为4×3=12.
所以,中奖这个事件包含的基本事件数为14.
因此,中奖概率为$\frac{7}{15}$.…(6分)
(2)设两人到达的时间分别为9点到10点之间的x分钟、y分钟.
用(x,y)表示每次试验的结果,则所有可能结果为Ω={(x,y)|0≤x≤40,20≤y≤60};
记甲比乙提前到达为事件A,则事件A的可能结果为A={(x,y)|x<y,0≤x≤40,20≤y≤60}.
如图所示,试验全部结果构成区域Ω为正方形ABCD.而事件A所构成区域是正方形内的阴影部分.
根据几何概型公式,得到P(A)=$\frac{4{0}^{2}-\frac{1}{2}×2{0}^{2}}{4{0}^{2}}$=$\frac{7}{8}$.
所以,甲比乙提前到达的概率为$\frac{7}{8}$.…(12分)
点评 本题考查了古典概型和几何概型的概率求法;关键字明确事件的表达方式,利用相关的公式解答.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,2] | B. | [1,2] | C. | [1,+∞) | D. | [2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (x+1)2+(y-1)2=6 | B. | (x-1)2+(y+1)2=6 | C. | (x+1)2+(y-1)2=3 | D. | (x-1)2+(y+1)2=3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若m∥α,n∥β,m⊥n,则α⊥β | B. | 若m∥n,n∥α,α∥β,则m∥β | ||
| C. | α∥β,m⊥α,n∥β⇒m⊥n | D. | 若α⊥β,α∩β=n,m⊥n,则m⊥α |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
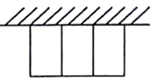 有一批材料可以建成80m的围墙,若用此材料在一边靠墙的地方围成一块矩形场地,中间用同样的材料隔成三个面积相等的小矩形(如图所示),且围墙厚度不计,则围成的矩形的最大面积为( )
有一批材料可以建成80m的围墙,若用此材料在一边靠墙的地方围成一块矩形场地,中间用同样的材料隔成三个面积相等的小矩形(如图所示),且围墙厚度不计,则围成的矩形的最大面积为( )| A. | 200m2 | B. | 360m2 | C. | 400m2 | D. | 480m2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com