Question

6．设f₀（x）=|x-1|-10，f_n（x）=|f_n-1（x）|-（n+1）（n∈N^*），则函数f₂₀（x）的零点之和为2．

Answer 1

分析 运用特殊函数f₀（x）=|x-1|-10=$\left\{\begin{array}{l}{x-11，x≥10}\\{-9-x，x＜1}\end{array}\right.$得出f₁（x）的图象判断其零点的方法，再思考f₂₀（x）=|f₂₀（x）|-21，零点的位置，及个数，即可得出答案．

解答 解：∵f₀（x）=|x-1|-10=$\left\{\begin{array}{l}{x-11，x≥10}\\{-9-x，x＜1}\end{array}\right.$
∴f₁（x）的图象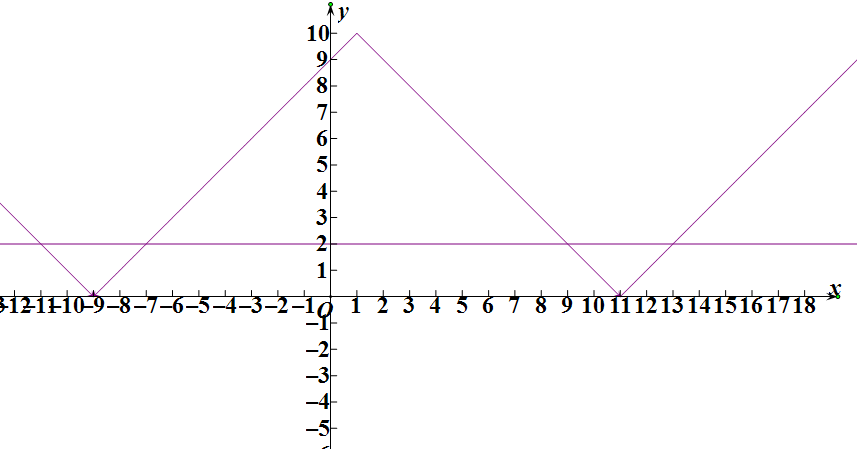
根据对称性得出零点的和为2×2=4，
f₁（x）=|f₀（x）|-2
根据对称性得出f₁（x）的零点的和为2×2=4，
∵f₂₀（x）=|f₂₀（x）|-21，
∴图象关于x=1对称，利用折点的数据可得出只有2个零点，关于x=1对称，
∴函数f₂₀（x）的零点之和为2

点评 本题考查了函数的零点问题，观察图象的能力，归纳能力，数学思维判断能力，属于中档题．