
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{5}$ |
分析 根据线段PF1与y轴的交点M恰好为线段PF1的中点,得到OM∥PF2,PF2⊥F1F2,结合直角三角形的边角关系进行求解即可.
解答 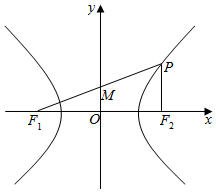 解∵线段PF1与y轴的交点M恰好为线段PF1的中点,
解∵线段PF1与y轴的交点M恰好为线段PF1的中点,
∴OM∥PF2,PF2⊥F1F2,
∵|OM|=b,∴|PF2|=2b,
∵|PF1|-|PF2|=2a,
∴|PF1|=|PF2|+2a=2a+2b=2(a+b),
在直角三角形PF1F2中,
4(a+b)2=4b2+4c2,
即(a+b)2=b2+c2,
即a2+2ab+b2=2b2+a2,
即2ab=b2,
b=2a,
则c2=a2+b2=a2+4a2=5a2,
即c=$\sqrt{5}$a,
则离心率e=$\frac{c}{a}$=$\sqrt{5}$,
故选:D
点评 本题主要考查双曲线离心率的计算,根据直径三角形的边角关系建立方程关系是解决本题的关键.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{5}$ | B. | 2 | C. | $\sqrt{2}+2$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
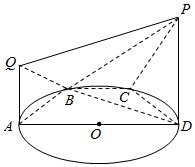 如图,等腰梯形ABCD的底角A等于60°,其外接圆圆心O在边AD上,直角梯形PDAQ垂直于圆O所在平面,∠QAD=∠PDA=90°,且AD=2AQ=4
如图,等腰梯形ABCD的底角A等于60°,其外接圆圆心O在边AD上,直角梯形PDAQ垂直于圆O所在平面,∠QAD=∠PDA=90°,且AD=2AQ=4查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 天数t(天) | 3 | 4 | 5 | 6 | 7 |
| 繁殖个数y(千个) | c | 3 | 4 | 4.5 | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{16}-\frac{y^2}{9}=1$ | B. | $\frac{y^2}{16}-\frac{x^2}{9}=1$ | C. | $\frac{x^2}{9}-\frac{y^2}{16}=1$ | D. | $\frac{y^2}{9}-\frac{x^2}{16}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 对任意n∈N*,P(n)是真命题 | |
| B. | 对任意n∈N*,仅有P(2n)是真命题 | |
| C. | 对任意n∈N*,仅有P(2n)和P(2n-1)是真命题 | |
| D. | 对任意n∈N*,P(n)不是真命题 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com