
分析 (1)由已知得f(x)+f(1-x)=$\frac{4^x}{{{4^x}+2}}+\frac{2}{{2+{4^x}}}$,由此能证明f(x)+f(1-x)=1.
(2)令S=$f({\frac{1}{2016}})+f({\frac{2}{2016}})+f({\frac{3}{2016}})+…+f({\frac{2014}{2016}})+f({\frac{2015}{2016}})$ ①,则S=f(${\frac{2015}{2016}}$)+f(${\frac{2014}{2016}}$)+f($\frac{2013}{2016}$)+…+f(${\frac{2}{2016}}$)+f(${\frac{1}{2016}}$)②,①+②,由此能求出结果.
解答 (1)证明:∵f(x)=$\frac{4^x}{{{4^x}+2}}$,
∴f(x)+f(1-x)=$\frac{4^x}{{{4^x}+2}}+\frac{{{4^{1-x}}}}{{{4^{1-x}}+2}}$=$\frac{4^x}{{{4^x}+2}}+\frac{4}{{4+2•{4^x}}}$
=$\frac{4^x}{{{4^x}+2}}+\frac{4}{{4+2•{4^x}}}$=$\frac{4^x}{{{4^x}+2}}+\frac{2}{{2+{4^x}}}$=1
(2)解:令S=$f({\frac{1}{2016}})+f({\frac{2}{2016}})+f({\frac{3}{2016}})+…+f({\frac{2014}{2016}})+f({\frac{2015}{2016}})$ ①
则S=$f({\frac{2015}{2016}})+f({\frac{2014}{2016}})+f({\frac{2013}{2016}})+…+f({\frac{2}{2016}})+f({\frac{1}{2016}})$ ②
两式相加,由(1)得,2S=2015,S=$\frac{2015}{2}$.
∴f(${\frac{1}{2016}}$)+f(${\frac{2}{2016}}$)+f(${\frac{3}{2016}}$)+…+f(${\frac{2014}{2016}}$)+f(${\frac{2015}{2016}}$)=$\frac{2015}{2}$.
点评 本题考查等式成立的证明,考查函数值的求法,解题时要认真审题,注意函数性质的合理运用,是中档题.


 全能闯关100分系列答案
全能闯关100分系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 正方形 | B. | 平行四边形 | C. | 正五边形 | D. | 正六边形 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{3}{2}$ | B. | -$\frac{2}{3}$ | C. | $\frac{2}{5}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
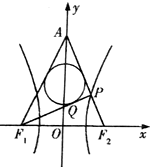 如图,已知双曲线$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1(a>0,b>0)的左、右焦点分别为F1,F2,|F1F2|=6,P是双曲线右支上的一点,F2P与y轴交于点A,△APF1的内切圆在边PF1上的切点为Q,若|PQ|=1,则双曲线的离心率是( )
如图,已知双曲线$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1(a>0,b>0)的左、右焦点分别为F1,F2,|F1F2|=6,P是双曲线右支上的一点,F2P与y轴交于点A,△APF1的内切圆在边PF1上的切点为Q,若|PQ|=1,则双曲线的离心率是( )| A. | 3 | B. | 2 | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com