
分析 令t(x)=$\frac{201{6}^{x}-1}{2(1+201{6}^{x})}$,判断其奇偶性,并求得t(x)=$\frac{1}{2}-\frac{1}{201{6}^{x}+1}$∈($-\frac{1}{2}$,$\frac{1}{2}$),然后分t(x)=0和t(x)≠0求解函数值域.
解答 解:∵f(x)=$\frac{201{6}^{x}}{1+201{6}^{x}}$,∴f(x)-$\frac{1}{2}$=$\frac{201{6}^{x}}{1+201{6}^{x}}$$-\frac{1}{2}$=$\frac{201{6}^{x}-1}{2(1+201{6}^{x})}$,
令t(x)=$\frac{201{6}^{x}-1}{2(1+201{6}^{x})}$,则t(-x)=$\frac{201{6}^{-x}-1}{2(1+201{6}^{-x})}=\frac{1-201{6}^{x}}{2(1+201{6}^{x})}$=-t(x),
即t(x)为奇函数,又t(x)=$\frac{1}{2}-\frac{1}{201{6}^{x}+1}$∈($-\frac{1}{2}$,$\frac{1}{2}$),
当t(x)=0时,[t(x)]+[t(-x)]=[f(x)-$\frac{1}{2}$]+[f(-x)-$\frac{1}{2}$]=0;
当t(x)≠0时,不妨设t(x)>0,则[t(x)]=0,[t(-x)]=-1,
则[t(x)]+[t(-x)]=[f(x)-$\frac{1}{2}$]+[f(-x)-$\frac{1}{2}$]=-1.
∴函数g(x)=[f(x)-$\frac{1}{2}$]+[f(-x)-$\frac{1}{2}$]的值域为{-1,0}.
故答案为:{-1,0}.
点评 本题考查函数值域的求法,考查函数奇偶性的性质,考查逻辑思维能力和推理运算能力,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | 12 | B. | 8 | C. | -8 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 身高x(cm) | 160 | 165 | 170 | 175 | 180 |
| 体重y(kg) | 66 | 67 | 70 | 73 | 74 |
| A. | 70.9kg | B. | 71.2kg | C. | 70.55kg | D. | 71.05kg |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
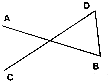
| A. | $\overrightarrow{AB}$-$\overrightarrow{CD}$ | B. | -$\frac{1}{2}$$\overrightarrow{AB}$+$\frac{1}{2}$$\overrightarrow{CD}$ | C. | $\frac{1}{2}$($\overrightarrow{AB}$-$\overrightarrow{CD}$) | D. | -($\overrightarrow{AB}$-$\overrightarrow{CD}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com