
| a |
| b |
| c |
| a |
| c |
| a |
| c |
| c |
| b |
| 5 |
| a |
| b |
| a |
| b |
| a |
| b |
|
|
|
| 5 |
| a•b |
| |a||b| |
12
| ||
| 25 |
|
|
|
| 3 |
| 5 |
| 4 |
| 5 |
| 3 |
| 5 |
| 4 |
| 5 |
| 5 |
| a•b |
| |a||b| |
12
| ||
| 25 |


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
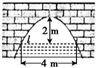 2013年国家加大了对环境污染监测力度,为此某市环保部门在市里的一条污水河的桥孔处进行了隔离封闭改造,桥孔的横断面为抛物线形(如下图所示),已知水面在l时,拱顶离水面2米,水面宽4米,则水上升0.5米后,水面宽变为
2013年国家加大了对环境污染监测力度,为此某市环保部门在市里的一条污水河的桥孔处进行了隔离封闭改造,桥孔的横断面为抛物线形(如下图所示),已知水面在l时,拱顶离水面2米,水面宽4米,则水上升0.5米后,水面宽变为查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com