考点:数列的求和,利用导数研究函数的单调性
专题:证明题,函数的性质及应用,导数的综合应用
分析:(Ⅰ)易求f′(x)=
-m,通过对m≤0与m>0的讨论,可求得函数f(x)的单调区间;
(Ⅱ)m=
,f(x)=
lnx-
x,?x
1,x
2∈[2,2e
2]都有g(x
1)≥f(x
2)成立等价于对?x∈[2,2e
2]都有[g(x)]
min≥[f(x)]
max,从而可求得实数a的取值范围为(0,3];
(Ⅲ)f(x)=
lnx-mx,m>0,令m=
,则f(x)=
lnx-
x,由(I)知f(x)在(0,1)单调递增,(1,+∞)单调递减,f(x)≤f(1)=-
,(当x=1时取“=”号)可得
lnx-
x≤-
,lnx≤x-1,于是2
2ln2+2
3ln3+…+2
nlnn<2
2×1+2
3×2+…+2
n×(n-1),利用错位相减法即可证得结论成立.
解答:
解:(I)f(x)=
lnx-mx,x>0,∴f′(x)=
-m(1分)
当m≤0时f′(x)>0,f(x)在(0,+∞)单调递增.(2分)
当m>0时,由f′(x)=0得x=
;
由
得0<x<
,
由
得x>
,(4分)
综上所述:当m≤0时,f(x)单调递增区间为(0,+∞).
当m>0时,f(x)单调递增区间为(0,
),单调递减区间为(
,+∞).(5分)
(Ⅱ)若m=
,f(x)=
lnx-
x,?x
1,x
2∈[2,2e
2]都有g(x
1)≥f(x
2)成立等价于对?x∈[2,2e
2]都有[g(x)]
min≥[f(x)]
max(6分)
由(I)知在[2,2e
2]上f(x)的最大值f(e
2)=
(7分)
g′(x)=1+
>0(a>0),x∈[2,2e
2].
函数g(x)在[2,2e
2]上是增函数,
[g(x)]
min=g(2)=2-
,(9分)
由2-
≥
,得a≤3,又因为a>0,∴a∈(0,3],
所以实数a的取值范围为(0,3].(10分)
(Ⅲ)证明:f(x)=
lnx-mx,m>0,令m=
,则f(x)=
lnx-
x,
由(I)知f(x)在(0,1)单调递增,(1,+∞)单调递减,
f(x)≤f(1)=-
,(当x=1时取“=”号)
∴
lnx-
x≤-
,lnx≤x-1(11分)
∴2
2ln2+2
3ln3+…+2
nlnn<2
2×1+2
3×2+…+2
n×(n-1)(12分)
令S=2
2×1+2
3×2+…+2
n×(n-1)…①
2S=2
3×1+2
4×2+…+2
n×(n-2)+…+2
n+1×(n-1)…②
①-②得-S=2
2+2
3+…+2
n-(n-1)×2
n+1=-4(1-2
n-1)-(n-1)×2
n+1,
∴S=4+(n-2)×2
n+1(n≥2且n∈N
*).
∴2
2ln2+2
3ln3+2
4ln4+…+2
nlnn<4+(n-2)×2
n+1(n≥2且n∈N
*).(14分)
点评:本小题主要考查函数、导数、数列、不等式等基础知识,考查推理论证能力、运算求解能力,考查数形结合思想、化归与转化思想、分类与整合思想,属于难题.




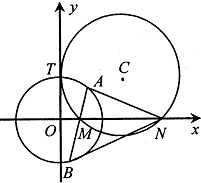 圆C与y轴切于点(0,2),与x轴正半轴交于两点M,N(点M在点N的左侧),且|MN|=3.
圆C与y轴切于点(0,2),与x轴正半轴交于两点M,N(点M在点N的左侧),且|MN|=3. 某路段属于限速路段,规定通过该路段的汽车时速不得超过70km/h,否则视为违规扣分,某天有1000辆汽车经过了该路段,经过雷达测速得到这些汽车运行时速的频率分布直方图,如图所示,则违规扣分的汽车大约为
某路段属于限速路段,规定通过该路段的汽车时速不得超过70km/h,否则视为违规扣分,某天有1000辆汽车经过了该路段,经过雷达测速得到这些汽车运行时速的频率分布直方图,如图所示,则违规扣分的汽车大约为