练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】设函数.

    (1)若当时，取得极值，求的值，并求的单调区间.

    (2)若存在两个极值点，求的取值范围，并证明：.

    【答案】（1），的单调增区间为，单调减区间为. （2），证明见解析

    【解析】

    （1）求导数，由题意可知为方程的根，求解值，即可.再令导数，，分别求解单调增区间与单调减区间，即可.

    （2）函数存在两个极值点，等价于方程即在上有两个不等实根，则，即可. 变形整理为；若证明不等式，则需证明，由变形为，不妨设，即证，令，则，求函数的取值范围，即可证明.

    （1）

    时，取得极值.

    .

    解得或

    解得

    的单调增区间为，单调减区间为.

    （2）

    存在两个极值点

    方程即在上有两个不等实根.

    ，

    .

    所证不等式等价于

    即

    不妨设，即证

    令，

    ，在上递增.

    成立.

    成立.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数，且曲线与直线相切于点，

    （1）求；

    （2）若，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系中，斜率为k的动直线l过点，以坐标原点O为极点，x轴的正半轴为极轴建立极坐标系，曲线C的极坐标方程为.

    （1）若直线l与曲线C有两个交点，求这两个交点的中点P的轨迹关于参数k的参数方程；

    （2）在条件（1）下，求曲线的长度.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】随着互联网金融的不断发展，很多互联网公司推出余额增值服务产品和活期资金管理服务产品，如蚂蚁金服旗下的“余额宝”，腾讯旗下的“财富通”，京东旗下“京东小金库”.为了调查广大市民理财产品的选择情况，随机抽取1100名使用理财产品的市民，按照使用理财产品的情况统计得到如下频数分布表：

    分组

    频数（单位：名）

    使用“余额宝”

    使用“财富通”

    使用“京东小金库”

    40

    使用其他理财产品

    60

    合计

    1100

    已知这1100名市民中，使用“余额宝”的人比使用“财富通”的人多200名.

    （1）求频数分布表中，的值；

    （2）已知2018年“余额宝”的平均年化收益率为，“财富通”的平均年化收益率为，“京东小金库”的平均年化收益率为，有3名市民，每个人理财的资金有10000元，且分别存入“余额宝”“财富通”“京东小金库”，求这3名市民2018年理财的平均年化收益率；

    （3）若在1100名使用理财产品的市民中，从使用“余额宝”和使用“财富通”的市民中按分组用分层抽样方法共抽取5人，然后从这5人中随机选取2人，求“这2人都使用‘财富通’”的概率.

    注：平均年化收益率，也就是我们所熟知的利率，理财产品“平均年化收益率为”即将100元钱存入某理财产品，一年可以获得3元利息.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

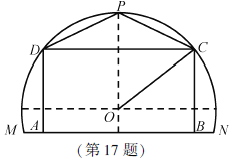
    【题目】某农场有一块农田，如图所示，它的边界由圆O的一段圆弧（P为此圆弧的中点）和线段MN构成．已知圆O的半径为40米，点P到MN的距离为50米．现规划在此农田上修建两个温室大棚，大棚Ⅰ内的地块形状为矩形ABCD，大棚Ⅱ内的地块形状为，要求均在线段上，均在圆弧上．设OC与MN所成的角为．

    （1）用分别表示矩形和的面积，并确定的取值范围；

    （2）若大棚Ⅰ内种植甲种蔬菜，大棚Ⅱ内种植乙种蔬菜，且甲、乙两种蔬菜的单位面积年产值之比为．求当为何值时，能使甲、乙两种蔬菜的年总产值最大．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，其中

    （Ⅰ）求的单调区间；

    （Ⅱ）若在上存在，使得成立，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）＝（x﹣a）cosx﹣sinx，g（x）x3ax2，a∈R

    （1）当a＝1时，求函数y＝f（x）在区间（0，）上零点的个数；

    （2）令F（x）＝f（x）+g（x），试讨论函数y＝F（x）极值点的个数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为了解某市高三数学复习备考情况，该市教研机构组织了一次检测考试，并随机抽取了部分高三理科学生数学成绩绘制如图所示的频率分布直方图.

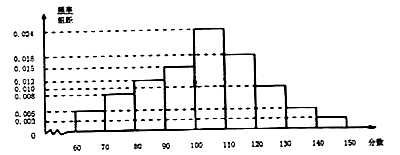
    （1）根据频率分布直方图，估计该市此次检测理科数学的平均成绩；（精确到个位）

    （2）研究发现，本次检测的理科数学成绩近似服从正态分布（，约为），按以往的统计数据，理科数学成绩能达到自主招生分数要求的同学约占.

    （ⅰ）估计本次检测成绩达到自主招生分数要求的理科数学成绩大约是多少分？（精确到个位）

    （ⅱ）从该市高三理科学生中随机抽取人，记理科数学成绩能达到自主招生分数要求的人数为，求的分布列及数学期望．（说明：表示的概率.参考数据：）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系中，曲线的参数方程为(为参数).以为极点，轴的正半轴为极轴建立极坐标系，直线的极坐标方程为()，将曲线向左平移2个单位长度得到曲线.

    （1）求曲线的普通方程和极坐标方程；

    （2）设直线与曲线交于两点，求的取值范围.

    查看答案和解析>>

    同步练习册答案