
分析 根据排列组合求出所抽取的2道题的基本事件共有15种,
(1)所抽取的2道题都是甲类题有3种,利用古典概型计算即可;
(2)所抽取的2道题不是同一类题的有9种,利用古典概型计算即可.
解答 解:知识竞赛中有6道题,其中3道甲类题A、B、C,3道乙类题X、Y、Z,张同学从中任意抽取2道解答题,共有${C}_{6}^{2}$=15种,
(1)所抽取的2道题都是甲类题有${C}_{3}^{2}$=3种,
故所抽取的2道题都是甲类题的概率P=$\frac{3}{15}$=$\frac{1}{5}$,;
(Ⅱ),所抽取的2道题不是同一类题的有${C}_{3}^{1}•{C}_{3}^{1}$=9种,
故所抽取的2道题不是同一类题的概率P=$\frac{9}{15}$=$\frac{3}{5}$.
点评 本题考查组合的运用以及古典概型的概率的计算,属于基础题


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | p∨q | C. | (¬p)∧q | D. | (¬p)∨q |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x>1} | B. | {x|0<x<1或1<x<+∞} | C. | {x|x>0} | D. | {x|x<0或x>1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x2+y2-2x+4y=0 | B. | x2+y2+2x+4y=0 | C. | x2+y2-2x-4y=0 | D. | x2+y2+2x-4y=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 0 | B. | $\sqrt{3}$ | C. | -$\sqrt{3}$ | D. | -$\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 甲 | 3 | 2 | 0 | 1 |
| 乙 | 4 | 3 | 2 | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
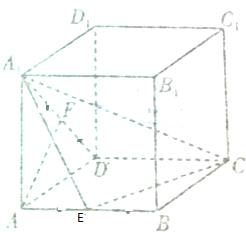 如图,在长方体ABCD-A1B1C1D1中,AD=AA1=3,AB=$\sqrt{6}$,E,F分别为AB,AD1的中点.求证:AF∥A1EC.
如图,在长方体ABCD-A1B1C1D1中,AD=AA1=3,AB=$\sqrt{6}$,E,F分别为AB,AD1的中点.求证:AF∥A1EC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com