
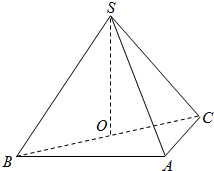
 如图,在三棱锥S-ABC中,侧面SAB、SAC均为边长为$\sqrt{2}$等边三角形,∠BAC=90°,O为BC中点.
如图,在三棱锥S-ABC中,侧面SAB、SAC均为边长为$\sqrt{2}$等边三角形,∠BAC=90°,O为BC中点.分析 (1)欲证SO⊥平面ABC,根据直线与平面垂直的判定定理可知只需证SO与平面ABC内两相交直线垂直,而SO⊥BC,SO⊥AO,又AO∩BO=O,满足定理条件;
(2)以O为坐标原点,射线OB,OA分别为x轴、y轴的正半轴,建立空间直角坐标系O-xyz,求出两法向量,利用向量法进行求解即可.
解答 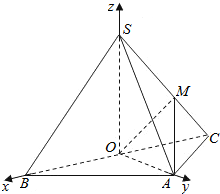 证明:(Ⅰ)∵侧面SAB、SAC均为边长为$\sqrt{2}$等边三角形,∠BAC=90°,O为BC中点,
证明:(Ⅰ)∵侧面SAB、SAC均为边长为$\sqrt{2}$等边三角形,∠BAC=90°,O为BC中点,
∴$OA=OB=OC=\frac{{\sqrt{2}}}{2}SA$=1,且AO⊥BC,
又△SBC为等腰三角形,故SO⊥BC,
且$SO=\frac{{\sqrt{2}}}{2}SA$=1,从而OA2+SO2=SA2.
即△SOA为直角三角形,SO⊥AO.
又AO∩BO=O.
∴SO⊥平面ABC.
(Ⅱ)解:以O为坐标原点,射线OB,OA分别为x轴、y轴的正半轴,
建立如图的空间直角坐标系O-xyz.
∵$OA=OB=OC=\frac{{\sqrt{2}}}{2}SA$=1
∴B(1,0,0),则C(-1,0,0),A(0,1,0),S(0,0,1).
SC的中点$M({-\frac{1}{2},0,\frac{1}{2}})$,$\overrightarrow{MO}=({\frac{1}{2},0,-\frac{1}{2}}),\overrightarrow{MA}=({\frac{1}{2},1,-\frac{1}{2}}),\overrightarrow{SC}=(-1,0,-1)$.
∴$\overrightarrow{MO}•\overrightarrow{SC}=0,\overrightarrow{MA}•\overrightarrow{SC}=0$.
故$MO⊥SC,MA⊥SC,<\overrightarrow{MO},\overrightarrow{MA}>$等于二面角A-SC-B的平面角.
$cos<\overrightarrow{MO},\overrightarrow{MA}>=\frac{{\overrightarrow{MO}•\overrightarrow{MA}}}{{|{\overrightarrow{MO}}|•|{\overrightarrow{MA}}|}}=\frac{{\sqrt{3}}}{3}$,
故二面角A-SC-B的余弦值为$\frac{{\sqrt{3}}}{3}$.
点评 本题主要考查直线与平面垂直,以及二面角等基础知识,考查空间想象能力,运算能力和推理论证能力.建立坐标系利用向量法是解决二面角的常用方法.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
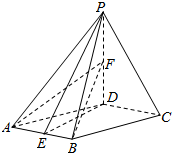 已知四棱锥P-ABCD,底面ABCD是菱形,∠DAB=60°,PD⊥平面ABCD,PA=AD,点E为AB中点,点F在线段PD上,且PF:FD=1:3.
已知四棱锥P-ABCD,底面ABCD是菱形,∠DAB=60°,PD⊥平面ABCD,PA=AD,点E为AB中点,点F在线段PD上,且PF:FD=1:3.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 甲、乙两名运动员在某项测试中的6次成绩的茎叶图如图所示,$\overline{x_1}$,$\overline{x{\;}_2}$分别表示甲、乙两名运动员这项测试成绩的平均数,$S_1^2$,$S_2^2$分别表示甲、乙两名运动员这项测试成绩的方差,则有( )
甲、乙两名运动员在某项测试中的6次成绩的茎叶图如图所示,$\overline{x_1}$,$\overline{x{\;}_2}$分别表示甲、乙两名运动员这项测试成绩的平均数,$S_1^2$,$S_2^2$分别表示甲、乙两名运动员这项测试成绩的方差,则有( )| A. | $\overline{x_1}$>$\overline{x{\;}_2}$,$S_1^2$<$S_2^2$ | B. | $\overline{x_1}$=$\overline{x{\;}_2}$,$S_1^2$>$S_2^2$ | ||
| C. | $\overline{x_1}$=$\overline{x{\;}_2}$,$S_1^2$=$S_2^2$ | D. | $\overline{x_1}$=$\overline{x{\;}_2}$,$S_1^2$<$S_2^2$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
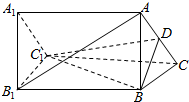 已知如图,ABC-A1B1C1是正三棱柱,D是AC的中点.
已知如图,ABC-A1B1C1是正三棱柱,D是AC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com