
分析 (1)由等比数列通项公式得a1a2…a18=(a5•a14)9=218,从而a5•a14=4,由此能求出公比q.
(2)由等比数列的通项公式得${{a}_{1}}^{18}$=$\frac{{2}^{18}}{{2}^{(9×17)}}$=2-135,S=a3a6a9…a18=a16•217,由此能求出a3a6a9…a18的值.
解答 解:(1)∵数列{an}是各项均为正数的等比数列,
且a1a2…a18=218,a5+a14=5,
∴a1a2…a18=(a5•a14)9=218,
∴a5•a14=4,
联立$\left\{\begin{array}{l}{{a}_{5}+{a}_{14}=5}\\{{a}_{5}•{a}_{14}=4}\end{array}\right.$,得a5=1,a14=4,或a14=1,a5=4,
当a5=1,a14=4时,${q}^{9}=\frac{{a}_{14}}{{a}_{5}}=4$,解得q=$\root{9}{4}$.
当a14=1,a5=4时,${q}^{9}=\frac{{a}_{14}}{{a}_{5}}$=$\frac{1}{4}$,解得q=$\root{9}{\frac{1}{4}}$.
(2)∵数列{an}是各项均为正数的等比数列,且a1a2…a18=218,公比q=2,
∴a1a2…a18=a118•2(9×17)=218,${{a}_{1}}^{18}$=$\frac{{2}^{18}}{{2}^{(9×17)}}$=2-135,
∴S=a3a6a9…a18=a16•217,
S3=a118•2(17×3)=2-135•251=2-84,
∴S=2-28.
∴a3a6a9•…•a18=2-28.
点评 本题考查等比数列的公比的求法,是中档题,解题时要认真审题,注意等比数列的性质的合理运用.


 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案科目:高中数学 来源: 题型:解答题
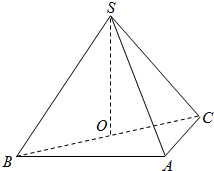 如图,在三棱锥S-ABC中,侧面SAB、SAC均为边长为$\sqrt{2}$等边三角形,∠BAC=90°,O为BC中点.
如图,在三棱锥S-ABC中,侧面SAB、SAC均为边长为$\sqrt{2}$等边三角形,∠BAC=90°,O为BC中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=sinx | B. | y=-|x-1| | C. | y=ex-e-x | D. | y=ln$\frac{1-x}{1+x}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com