
| A. | -3 | B. | ±3 | C. | 4 | D. | ±4 |
分析 求出f(x)的周期及对称中心,作出f(x)的函数图象草图,利用对称性得出四个根之和.
解答 解:∵f(x-2)=-f(x),∴f(x)=-f(x+2),
∴f(x+2)=f(x-2),∴f(x)的周期为4.
又f(x-1)关于(1,0)对称,∴f(x)的图象关于(0,0)对称,
∴f(x)是奇函数.
作出f(x)的大致函数图象如图所示: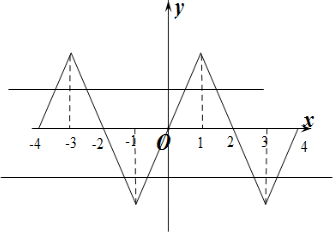
设方程f(x)=m在区间[-4,4]上有4个不同的根从小到大依次为a,b,c,d,
当m>0,a+b=-6,c+d=2,∴a+b+c+d=-4,
当m<0时,a+b=-2,c+d=6,∴a+b+c+d=4.
故选:D.
点评 本题考查了函数的周期性,对称性与函数零点的关系,属于中档题.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:选择题
| P(k2>k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.83 |
| A. | 6.785 | B. | 5.802 | C. | 9.697 | D. | 3.961 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ∅ | B. | R | C. | B | D. | A |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{2}{3}$ | B. | -2 | C. | 0 | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com