
分析 首先根据抛物线方程,求得焦点坐标为F( $\frac{9}{4}$,0),从而设所求直线方程为y=k(x-$\frac{9}{4}$).再将所得方程与抛物线y2=9x消去y,利用韦达定理求出x1+x2,最后结合直线过抛物线y2=9x焦点截得弦长为12,得到x1+x2+3=12,求出k,得到直线的倾斜角.
解答 解:∵抛物线方程是y2=9x,
∴2p=9,可得 $\frac{p}{2}$=$\frac{9}{4}$,焦点坐标为F($\frac{9}{4}$,0)
设所求直线方程为y=k(x-$\frac{9}{4}$),
与抛物线y2=9x消去y,得k2x2-($\frac{9}{2}$k2+9)x+$\frac{81}{16}$k2=0
设直线交抛物线与A(x1,y1),B(x2,y2),
由根与系数的关系,得x1+x2=$\frac{\frac{9}{2}{k}^{2}+9}{{k}^{2}}$,
∵直线过抛物线y2=9x焦点,交抛物线得弦长为12,
∴x1+x2+$\frac{9}{2}$=12,可得x1+x2=$\frac{15}{2}$,
因此,$\frac{\frac{9}{2}{k}^{2}+9}{{k}^{2}}$=$\frac{15}{2}$,解之得k2=3,
∴k=tanα=±$\sqrt{3}$,结合α∈[0,π),可得α=$\frac{π}{3}$或$\frac{2π}{3}$.
故答案为:$\frac{π}{3}$或$\frac{2π}{3}$.
点评 本题给出已知方程的抛物线焦点弦长为12,求这条弦所在直线的倾斜角,着重考查了直线倾斜角、抛物线的基本概念和直线与抛物线的位置关系等知识点,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
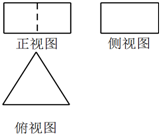 如图为某几何体的三视图,其中俯视图为边长为2的正三角形,正视图为长为2,宽为1的矩形,则该三视图的体积为$\sqrt{3}$,表面积为$6+2\sqrt{3}$.
如图为某几何体的三视图,其中俯视图为边长为2的正三角形,正视图为长为2,宽为1的矩形,则该三视图的体积为$\sqrt{3}$,表面积为$6+2\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
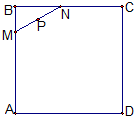 正方形ABCD的边长为2,(如图),线段MN=1,当点M、N在正方形ABCD的边上滑动一周(保持MN的长度不变)时,线段MN的中点P的轨迹围成一个封闭图形E,现向正方形中随机投入一点,则该点落在E内的概率是( )
正方形ABCD的边长为2,(如图),线段MN=1,当点M、N在正方形ABCD的边上滑动一周(保持MN的长度不变)时,线段MN的中点P的轨迹围成一个封闭图形E,现向正方形中随机投入一点,则该点落在E内的概率是( )| A. | $\frac{7}{8}$ | B. | $\frac{π}{16}$ | C. | $1-\frac{π}{16}$ | D. | $\frac{3}{4}+\frac{π}{16}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1,-1) | B. | (0,-1,6) | C. | (0,1,-6) | D. | (0,1,6) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$ | B. | -1 | C. | $\frac{1}{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | α<β | B. | cosα<cosβ | C. | tanα<tanβ | D. | sinα>sinβ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{9}{4}$ | B. | -$\frac{4}{9}$ | C. | -$\frac{3}{8}$ | D. | 不存在 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com