
分析 根据极值的概念,求出a,b值,利用导函数判断函数的单调区间,根据单调区间判断函数的极值.
解答 解:f(x)=alnx+bx2+x,
f'(x)=$\frac{a}{x}$+2bx+1,
∵f'(1)=0,f'(2)=0,
∴a=-$\frac{2}{3}$,b=-$\frac{1}{6}$;
f'(x)=-$\frac{{x}^{2}-3x+2}{3x}$,
当x在(0,1)时,f'(x)<0,f(x)递减,
当x在(1,2)时,f'(x)>0,f(x)递增,
当x在(2,+∞)时,f'(x)<0,f(x)递减,
∴f(x)在x1与处取得极小值,在x2处取得极大值.
点评 考查了函数极值的概念和导函数的应用.


科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$-1 | B. | $\sqrt{3}$-1 | C. | $\frac{{\sqrt{2}-1}}{2}$ | D. | $\frac{{\sqrt{3}-1}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①④ | B. | ①③ | C. | ②③ | D. | ③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
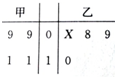 从巍山县庙街镇一所小学的甲、乙两个班级分别随机抽取4名学生的年龄制作出如右所示茎叶图,乙纪录中有一个数据模糊,无法确认,以X表示.
从巍山县庙街镇一所小学的甲、乙两个班级分别随机抽取4名学生的年龄制作出如右所示茎叶图,乙纪录中有一个数据模糊,无法确认,以X表示.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
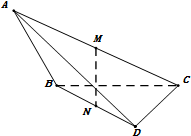 如图,在三棱锥A-BCD中,二面角A-BC-D的大小为$\frac{π}{4}$,AB⊥BC,DC⊥BC,M,N分别为AC,BD的中点,已知AB=$\sqrt{2}$,BC=CD=1.
如图,在三棱锥A-BCD中,二面角A-BC-D的大小为$\frac{π}{4}$,AB⊥BC,DC⊥BC,M,N分别为AC,BD的中点,已知AB=$\sqrt{2}$,BC=CD=1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com