考点:直线与平面垂直的判定,直线与平面平行的判定
专题:证明题,空间位置关系与距离
分析:(1)连接AD1,由已知可证四边形ABC1D1为平行四边形,即有A1D∥BC1,可证得EF∥BC1,又EF?平面C1BD,BC1?平面C1BD,从而可证EF∥平面AB1D1.
(2)连接AC,则AC⊥BD.可证AA1⊥平面ABCD,又AA1⊥BD,又AA1∩AC=A,可证BD⊥平面AA1C,有A1C⊥BD.同理可证A1C⊥BC1,又BD∩BC1=B,即可证明A1C⊥平面C1BD.
解答:
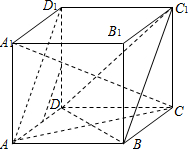
证明:(1)连接AD
1,
∵E,F分别是AD和DD
1的中点,
∴EF∥AD
1∵正方体ABCD-A
1B
1C
1D
1,
∴AB∥D
1C
1,AB=D
1C
1,
∴四边形ABC
1D
1为平行四边形,即有A
1D∥BC
1∴EF∥BC
1.
又EF?平面C
1BD,BC
1?平面C
1BD,
∴EF∥平面AB
1D
1.
(2)连接AC,则AC⊥BD.
∵正方体ABCD-A
1B
1C
1D
1,∴AA
1⊥平面ABCD,
∴AA
1⊥BD
又AA
1∩AC=A,∴BD⊥平面AA
1C,
∴A
1C⊥BD.
同理可证A
1C⊥BC
1,
又BD∩BC
1=B,
∴A
1C⊥平面C
1BD.
点评:本题考查的知识点是直线与平面平行的判定,直线与平面垂直的判定,直线与平面垂直的性质,熟练掌握空间线线,线面垂直及平行的判定定理,性质定理及几何特征是解答此类问题的关键.

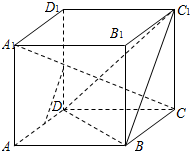 如图,在正方体ABCD-A1B1C1D1中,E,F分别是AD,DD1中点.求证:(1)EF∥平面C1BD;
如图,在正方体ABCD-A1B1C1D1中,E,F分别是AD,DD1中点.求证:(1)EF∥平面C1BD; 证明:(1)连接AD1,
证明:(1)连接AD1,

 华东师大版一课一练系列答案
华东师大版一课一练系列答案