
分析 延长F2M交PF1于点N,由题意可知△PNF2为等腰三角形,得OM是△PF1F2的中位线.利用三角形中位线定理和椭圆的定义,算出|OM|=a-|PF2|,再由椭圆的焦半径|PF2|的取值范围加以计算,即可得到|OM|的取值范围.
解答 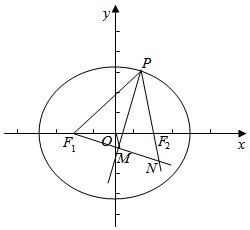 解:如图,延长PF2、F1M,交与N点,连接OM
解:如图,延长PF2、F1M,交与N点,连接OM
∵$\overrightarrow{PM}$=λ(${\frac{{\overrightarrow{P{F_1}}}}{{|{\overrightarrow{P{F_1}}}|}}$+$\frac{{\overrightarrow{P{F_2}}}}{{|{\overrightarrow{P{F_2}}}|}}}$),且$\overrightarrow{{F_1}M}$•$\overrightarrow{MP}$=0,
∴PM是∠F1PF2,且F1M⊥MP,
∴|PN|=|PF1|,M为F1F2中点,
∵O为F1F2中点,M为F1N中点
∴|OM|=$\frac{1}{2}$|F2N|=$\frac{1}{2}$||PN|-|PF2||=$\frac{1}{2}$||PF1|-|PF2||
设P点坐标为(x0,y0)
∵在椭圆$\frac{x^2}{16}$+$\frac{y^2}{8}$=1,离心率e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$
由圆锥曲线的统一定义,得|PF1|=a+ex0,|PF2|=a-ex0,
∴||PF1|-|PF2||=|a+ex0+a-ex0|=|2ex0|=$\sqrt{2}$|x0|
∵P点在椭圆$\frac{x^2}{16}$+$\frac{y^2}{8}$=1上,∴|x0|∈[0,4],
又∵x≠0,y≠0,可得|x0|∈(0,4),∴|OM|∈(0,2$\sqrt{2}$).
故答案为:(0,2$\sqrt{2}$).
点评 本题给出椭圆焦点三角形角平分线的垂线,求垂足到椭圆中心距离的范围.着重考查了椭圆的定义与简单几何性质、等腰三角形的判定与性质和三角形中位线定理等知识,属于中档题.


 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:高中数学 来源: 题型:选择题
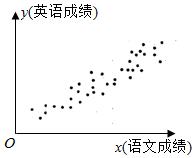 为研究语文成绩和英语成绩之间是否具有线性相关关系,统计两科成绩得到如图所示的散点图(两坐标轴单位长度相同),用回归直线$\hat y$=$\hat b$x+$\hat a$近似地刻画其相关系,根据图形,以下结论最有可能成立的是( )
为研究语文成绩和英语成绩之间是否具有线性相关关系,统计两科成绩得到如图所示的散点图(两坐标轴单位长度相同),用回归直线$\hat y$=$\hat b$x+$\hat a$近似地刻画其相关系,根据图形,以下结论最有可能成立的是( )| A. | 线性相关关系较强,b的值为3.25 | B. | 线性相关关系较强,b的值为0.83 | ||
| C. | 线性相关关系较强,b的值为-0.87 | D. | 线性相关关系太弱,无研究价值 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
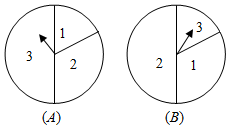 如图是两个独立的转盘(A)、(B),在两个图中三个扇形区域的圆心角分别为60°、120°、180°.用这两个转盘进行游戏,规则是:同时转动两个转盘待指针停下(当两个转盘中任意一个指针恰好落在分界线时,则这次转动无效,重新开始),记转盘(A)指针所对的区域为x,转盘(B)指针所对的区域为y,x、y∈{1,2,3},设x+y的值为ξ.
如图是两个独立的转盘(A)、(B),在两个图中三个扇形区域的圆心角分别为60°、120°、180°.用这两个转盘进行游戏,规则是:同时转动两个转盘待指针停下(当两个转盘中任意一个指针恰好落在分界线时,则这次转动无效,重新开始),记转盘(A)指针所对的区域为x,转盘(B)指针所对的区域为y,x、y∈{1,2,3},设x+y的值为ξ.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com