
分析 由曲线C的极坐标方程,求出曲线C的直角坐标方程为$\frac{{x}^{2}}{9}+\frac{{y}^{2}}{4}=1$,从而得到$\left\{\begin{array}{l}{x=3cosα}\\{y=2sinα}\end{array}\right.,0≤α<2π$,由此能求出3x+4y的最大值.
解答 解:∵曲线C的极坐标方程为${ρ^2}=\frac{36}{{4{{cos}^2}θ+9{{sin}^2}θ}}$,
∴4ρ2+5ρ2sin2θ=36,
∴4x2+9y2=36,即$\frac{{x}^{2}}{9}+\frac{{y}^{2}}{4}=1$,
∵P(x,y)是曲线C上的一个动点,∴$\left\{\begin{array}{l}{x=3cosα}\\{y=2sinα}\end{array}\right.,0≤α<2π$,
∴3x+4y=9cosα+8sinα=$\sqrt{145}$sin(α+γ),其中tanγ=$\frac{9}{8}$.
∴3x+4y的最大值为$\sqrt{145}$.
点评 本题考查代数式的最大值的求法,是中档题,解题时要认真审题,注意极坐标方程、直角坐标方程、参数方程的性质及互化公式的合理运用.


科目:高中数学 来源: 题型:解答题
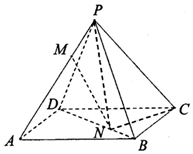 如图,已知正四棱锥P-ABCD中,PA=AB=2,点M,N分别在PA,BD上,且$\frac{PM}{PA}$=$\frac{BN}{BD}$=$\frac{1}{3}$.
如图,已知正四棱锥P-ABCD中,PA=AB=2,点M,N分别在PA,BD上,且$\frac{PM}{PA}$=$\frac{BN}{BD}$=$\frac{1}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 22 | B. | 20 | C. | 17 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
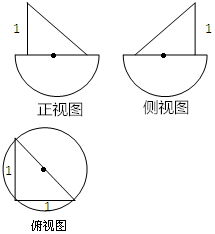 已知某几何体的三视图如图所示,其中正视图、侧视图均由直角三角形中与半圆构成,俯视图由圆和内接三角形构成,根据图中的数据可得几何体的表面积为( )
已知某几何体的三视图如图所示,其中正视图、侧视图均由直角三角形中与半圆构成,俯视图由圆和内接三角形构成,根据图中的数据可得几何体的表面积为( )| A. | 1+$\frac{\sqrt{3}+3π}{2}$ | B. | $\frac{1+\sqrt{3}+π}{2}$ | C. | $\frac{1+\sqrt{3}+3π}{2}$ | D. | $\frac{3+\sqrt{3}+3π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com