
分析 (1)根据|PF|=|PM|可知P的轨迹为以F为焦点,以y=-1为准线的抛物线;
(2)求出PQ的方程,联立方程组消元,根据根与系数的关系和弦长公式计算|PQ|,PQ的中点N,|NF|,通过比较|NF|与$\frac{1}{2}$|PQ|的大小得出结论.
解答 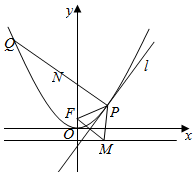 解:(I)∵P在FM的中垂线l上,∴|PF|=|PM|
解:(I)∵P在FM的中垂线l上,∴|PF|=|PM|
∵PM与直线y=-1垂直,∴|PM|为P到直线y=-1的距离.
∴P到点F(0,1)的距离与P到直线y=-1的距离相等,
∴P的轨迹为以(0,1)为焦点,以直线y=-1为准线的抛物线.
∴P的轨迹方程为:x2=4y.
(II)不妨设a>0,
∵△PFM为正三角形,∴直线FM的倾斜角为150°,即kFM=tan150°=-$\frac{\sqrt{3}}{3}$.
∴直线FM的方程为:y=-$\frac{\sqrt{3}}{3}$x+1,
令y=-1,得-$\frac{\sqrt{3}}{3}x+1$=-1,解得x=2$\sqrt{3}$,即M(2$\sqrt{3}$,0).
把x=2$\sqrt{3}$代入x2=4y得y=3.∴P(2$\sqrt{3}$,3).
∵l⊥FM,l⊥PQ,
∴FM∥PQ,∴kPQ=kFM=-$\frac{\sqrt{3}}{3}$.
∴直线PQ的方程为:y-3=-$\frac{\sqrt{3}}{3}$(x-2$\sqrt{3}$),即x+$\sqrt{3}$y-5$\sqrt{3}$=0.
联立方程组$\left\{\begin{array}{l}{x+\sqrt{3}y-5\sqrt{3}=0}\\{{x}^{2}=4y}\end{array}\right.$,消元得:$\sqrt{3}$x2+4x-20$\sqrt{3}$=0,
∴x1+x2=-$\frac{4\sqrt{3}}{3}$,x1x2=-20.y1+y2=$\frac{{{x}_{1}}^{2}+{{x}_{2}}^{2}}{4}$=$\frac{({x}_{1}+{x}_{2})^{2}-2{x}_{1}{x}_{2}}{4}$=$\frac{34}{3}$.
∴|PQ|=$\sqrt{1+\frac{1}{3}}$$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\frac{32}{3}$.∴以PQ为直径的圆的半径r=$\frac{16}{3}$.
设PQ的中点为N,则N(-$\frac{2\sqrt{3}}{3}$,$\frac{17}{3}$).
∴|NF|=$\sqrt{(\frac{2\sqrt{3}}{3})^{2}+(\frac{14}{3})^{2}}$=$\frac{4\sqrt{13}}{3}$.
∵$\frac{4\sqrt{13}}{3}$<$\frac{16}{3}$,
∴点F在以线段PQ为直径的圆内.
点评 本题考查了抛物线的定义,直线与圆锥曲线的位置关系,属于中档题.


科目:高中数学 来源: 题型:选择题
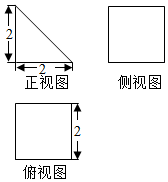 如图是一个正方体被一个平面截去一部分后得到的几何体的三视图,则该几何体的体积是原正方体的体积的( )
如图是一个正方体被一个平面截去一部分后得到的几何体的三视图,则该几何体的体积是原正方体的体积的( )| A. | $\frac{3}{4}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
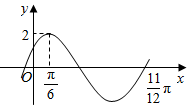 函数f(x)=sin(ωx+φ)(ω>0,0<φ<π)的部分图象如图所示.
函数f(x)=sin(ωx+φ)(ω>0,0<φ<π)的部分图象如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com