
分析 (1)利用代入法求C2的方程;
(2)求出射线θ=$\frac{π}{4}$与C1的交点A的极径为ρ1=2;与C2的交点B的极径为ρ2=4,即可得出结论.
解答 解:(1)设P(x,y),则由条件知M($\frac{x}{2}$,$\frac{y}{2}$),由于点M在C1上,所以$\frac{x}{2}$=$\sqrt{2}cosα$,$\frac{y}{2}$=$\sqrt{2}+\sqrt{2}sinα$
从而C2的方程为$\left\{\begin{array}{l}{x=2\sqrt{2}cosα}\\{y=2\sqrt{2}+2\sqrt{2}sinα}\end{array}\right.$(α为参数)-----6分
(2)曲线C1的极坐标方程为$ρ=2\sqrt{2}sinθ$,曲线C2的极坐标方程为$ρ=4\sqrt{2}sinθ$
射线θ=$\frac{π}{4}$与C1的交点A的极径为ρ1=2
射线θ=$\frac{π}{4}$与C2的交点B的极径为ρ2=4
所以|AB|=|ρ1-ρ2|=2-----12分
点评 本题考查轨迹方程,考查极坐标方程的运用,属于中档题.


 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $m<\frac{5}{2}$ | B. | $m>\frac{5}{2}$ | C. | m<2 | D. | m>2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
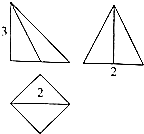
| A. | $\frac{13π}{4}$ | B. | $\frac{{\sqrt{13}π}}{2}$ | C. | 13π | D. | $\sqrt{13}π$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,2,3,4} | B. | {-4,1,2,3} | C. | {1,2,3} | D. | {-1,4,2} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | b>a>c | C. | c>a>b | D. | a>c>b |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,2] | B. | [0,2] | C. | [-2,2] | D. | (-2,2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com