
分析 (Ⅰ)求出函数的导数,通过讨论a的范围,求出函数的单调区间即可;
(Ⅱ)令F(x)=f(x)+(a+1)x+1-e,求出函数的导数,通过讨论a的范围,求出函数的单调区间,从而求出函数F(x)的最大值,进而确定a的范围即可;
(Ⅲ)令a=1则f(x)=lnx-x,根据函数的单调性得到lnx<x,对x取值,累加即可.
解答 解:(Ⅰ)${f^'}(x)=\frac{a}{x}-a=a(\frac{1}{x}-1)=a\frac{(1-x)}{x}$
当a>0时,f(x)的单调增区间为(0,1],单调减区间为[1,+∞);
当a<0时,f(x)的单调增区间为[1,+∞),单调减区间为(0,1];
(Ⅱ)令F(x)=f(x)+(a+1)x+1-e=alnx+x+1-e
F′(x)=$\frac{x+a}{x}$=0,若-a≤e,a≥-e,F(x) 在[e,e2]是增函数,
$F{(x)_{max}}=F({e^2})=2a+{e^2}-e+1≤0,a≤\frac{{e-1-{e^2}}}{2}$无解.
若e<-a≤e2,-e2≤a<-e,F(x)在[e,-a]是减函数;x∈[-a,e2]是增函数,
F(e)=a+1≤0,a≤-1,.$F({e^2})=2a+{e^2}-e+1≤0,a≤\frac{{e-1-{e^2}}}{2}$
∴-e2≤a≤$\frac{e-1{-e}^{2}}{2}$,若-a>e2,a<-e2,F(x)x∈[e,e2]是减函数,
F(x)max=F(e)=a+1≤0,a≤-1,∴a<-e2,
综上所述a≤$\frac{e-1{-e}^{2}}{2}$ (或用参数分离法)
(Ⅲ)令a=1则f(x)=lnx-x
由(1)知f(x)在[1,+∞)上单调递减,又因为
f(1)<0,所以有lnx<x,
即ln2<2,ln3<3…lnn<n,
∴$lnn!≤\frac{(n+2)(n-1)}{2}$.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及不等式的证明,是一道中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -1 | C. | 0 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{4}{5}$ | C. | -1 | D. | $-\frac{3}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
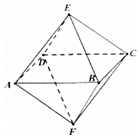
| A. | 不平行的两条棱所在的直线所成的角是60o或90o | |
| B. | 四边形AECF是正方形 | |
| C. | 点A到平面BCE的距离为$\frac{\sqrt{6}}{3}$ | |
| D. | 该八面体的顶点不会在同一个球面上. |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | d<0 | B. | a7=0 | ||
| C. | S${\;}_{{9}_{\;}}$>S5 | D. | S6和S7均为Sn的最大值 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com