Question

19．如图，已知一个八面体的各条棱长均为1，四边形ABCD 为正方形，则下列命题中的假命题是（　　）

• A． 不平行的两条棱所在的直线所成的角是60^o或90^o
• B． 四边形AECF是正方形
• C． 点A到平面BCE的距离为$\frac{\sqrt{6}}{3}$
• D． 该八面体的顶点不会在同一个球面上．

Answer 1

分析 对4个命题分别进行判断，即可得出结论．

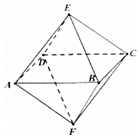
解答 解：因为八面体的各条棱长均为1，四边形ABCD为正方形，
所以在四棱锥E-ABCD中，相邻两条侧棱所成的角为60°，而像AE与CE所成的角为90°，A正确
因为AE=CE=1，AC=$\sqrt{2}$，满足勾股定理的逆定理，所以AE⊥CE，同理AF⊥CF，AE⊥AF，所以四边形AECF是正方形；故B正确；
设点A到平面BCE的距离h，由V_E-ABCD=2V_A-BCE，
所以$\frac{1}{3}×1×1×\frac{\sqrt{2}}{2}=2×\frac{1}{3}×\frac{\sqrt{3}}{4}h$，解得h=$\frac{\sqrt{6}}{3}$；
所以点A到平面BCE的距离$\frac{\sqrt{6}}{3}$；故C正确；
该八面体的顶点会在同一个球面上，球心为ABCD的中心，故不正确．
故选：D．

点评 本题考查了立体几何中线线关系以及线面关系，利用了等积法求点到平面的距离．