
 如图,在三棱柱ABC-A1B1C1中,E,F,G,H分别是AB,AC,A1B1,A1C1的中点,求证:
如图,在三棱柱ABC-A1B1C1中,E,F,G,H分别是AB,AC,A1B1,A1C1的中点,求证:分析 (1)由已知条件条件出EF∥平面BCGH,A1E∥平面BCHG,由此能证明平面平面EFA1∥平面BCHG;
(2)BG与CH必相交,设交点为P,证明P∈直线AA1,即可证明BG、CH、AA1三线共点.
解答 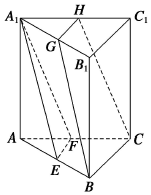 证明:(1)∵E,F分别为AB,AC的中点,∴EF∥BC,
证明:(1)∵E,F分别为AB,AC的中点,∴EF∥BC,
∵EF?平面BCHG,BC?平面BCHG,
∴EF∥平面BCHG.
∵A1G与EB平行且相等,
∴四边形A1EBG是平行四边形,
∴A1E∥GB,
∵A1E?平面BCHG,GB?平面BCHG,
∴A1E∥平面BCHG.
∵A1E∩EF=E,∴平面EFA1∥平面BCHG.
(2)∵GH∥BC,GH<BC,
∴BG与CH必相交,
设交点为P,
则由P∈BG,BG?平面BAA1B1,得P∈平面BAA1B1,
同理P∈平面CAA1C1,
又平面BAA1B1∩平面CAA1C1=AA1,
∴P∈直线AA1,∴BG、CH、AA1三线共点.
点评 本题考查平面与平面平行的证明,考查直线位置关系,是中档题,


 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{4}{5}$ | C. | -1 | D. | $-\frac{3}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
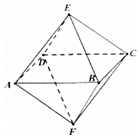
| A. | 不平行的两条棱所在的直线所成的角是60o或90o | |
| B. | 四边形AECF是正方形 | |
| C. | 点A到平面BCE的距离为$\frac{\sqrt{6}}{3}$ | |
| D. | 该八面体的顶点不会在同一个球面上. |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,3] | B. | [3,+∞) | C. | (1,2] | D. | [2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-4,3) | B. | (-4,3] | C. | (3,4] | D. | (3,4) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{8}{15}$ | C. | $\frac{16}{31}$ | D. | $\frac{16}{29}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com