
分析 (1)求导数,确定切线的斜率,可得曲线f(x)在点(1,f(1))处切线方程;
(2)求导,分类讨论,利用导数的正负讨论f(x)的单调性.
解答 解:(1)k=2时,f(x)=ln(1+x)-x+x2,f′(x)=$\frac{1}{1+x}$-1+2x
由于f(1)=ln(2),f′(1)=$\frac{3}{2}$,
所以曲线y=f(x)在点(1,f(1))处的切线方程为
y-ln2=$\frac{3}{2}$(x-1).即3x-2y+2ln2-3=0
(2)f'(x)=$\frac{x(kx+k-1)}{1+x}$,x∈(-1,+∞)
当k=0时,f′(x)=-$\frac{x}{1+x}$,
因此在区间(-1,0)上,f'(x)>0;在区间(0,+∞)上,f'(x)<0;
所以f(x)的单调递增区间为(-1,0),单调递减区间为(0,+∞);
当0<k<1时,f′(x)=$\frac{x(kx+k-1)}{1+x}$=0,得x1=0,x2=$\frac{1-k}{k}$>0;
因此,在区间(-1,0)和($\frac{1-k}{k}$,+∞)上,f'(x)>0;在区间(0,$\frac{1-k}{k}$)上,f'(x)<0;
即函数f(x)的单调递增区间为(-1,0)和($\frac{1-k}{k}$,+∞),单调递减区间为(0,$\frac{1-k}{k}$);
当k=1时,f′(x)=$\frac{{x}^{2}}{1+x}$.f(x)的递增区间为(-1,+∞)
当k>1时,由f′(x)=$\frac{x(kx+k-1)}{1+x}$=0,得x1=0,x2=$\frac{1-k}{k}$∈(-1,0);
因此,在区间(-1,$\frac{1-k}{k}$)和(0,+∞)上,f'(x)>0,在区间($\frac{1-k}{k}$,0)上,f'(x)<0;
即函数f(x)的单调递增区间为(-1,$\frac{1-k}{k}$)和(0,+∞),单调递减区间为($\frac{1-k}{k}$,0).
点评 本题考查导数知识的运用,考查导数的几何意义,考查函数的单调性,考查分类讨论的数学思想,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | 35 | 40 | 45 | 50 |
| y | 56 | 41 | 28 | 11 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在三棱柱ABC-A1B1C1中,E,F,G,H分别是AB,AC,A1B1,A1C1的中点,求证:
如图,在三棱柱ABC-A1B1C1中,E,F,G,H分别是AB,AC,A1B1,A1C1的中点,求证:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
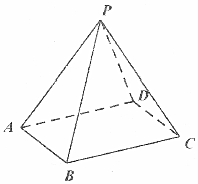 在底面是菱形的四棱锥P-ABCD中,∠BAD=60°,AB=2,PA=PC=2,PB=PD=$\sqrt{2}$.
在底面是菱形的四棱锥P-ABCD中,∠BAD=60°,AB=2,PA=PC=2,PB=PD=$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
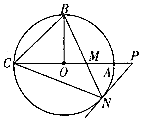 如图,圆O的半径OB垂直于直径AC,M为AO上一点,BM的延长线交圆O于点N,过点N的切线交CA的延长线于点P,连接BC,CN.
如图,圆O的半径OB垂直于直径AC,M为AO上一点,BM的延长线交圆O于点N,过点N的切线交CA的延长线于点P,连接BC,CN.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com