
| x | 35 | 40 | 45 | 50 |
| y | 56 | 41 | 28 | 11 |
���� ��1����ɢ��ͼ���Ӷ�ȷ��y��x����������ع�ϵ��
��2����35��56+40��41+45��28+50��11=5410��$\overline{x}$=42.5��$\overline{y}$=34��352+402+452+502=7350���Ӷ���$\widehat{a}$��$\widehat{b}$��
��3�������⣬P=��x-30��y=��x-30����-2.96x+159.8��=-2.96x2+248.6x-4794����31��x��53��x��N�����Ӷ�����ֵ�㣮
��� �⣺��1����ɢ��ͼ����ͼ��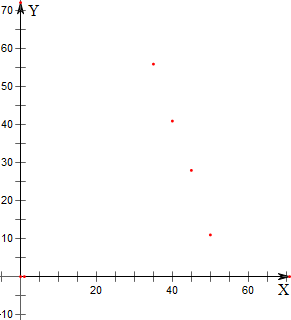
y��x����������ع�ϵ��
��2��35��56+40��41+45��28+50��11=5410��$\overline{x}$=42.5��$\overline{y}$=34��
352+402+452+502=7350��
��$\widehat{b}$=$\frac{5410-4��42.5��34}{7350-4��42��{5}^{2}}$=-2.96��
��$\widehat{a}$=34+2.96��42.5=159.8��
�����Իع鷽��Ϊy=-2.96x+159.8��
��3����y=-2.96x+159.8��0�ã�x��53��
P=��x-30��y
=��x-30����-2.96x+159.8��
=-.296x2+248.6x-4794����31��x��53��x��N����
�ʵ�x=$\frac{248.6}{2��2.96}$��42��
��Ԥ����۵���Ϊ42Ԫʱ�����ܻ���������������
���� ���⿼�������Թ滮��Ӧ�ü�����������Ӧ�ã������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | $\frac{4}{5}$ | C�� | -1 | D�� | $-\frac{3}{5}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0 | B�� | 1 | C�� | 2 | D�� | 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��1��3] | B�� | [3��+�ޣ� | C�� | ��1��2] | D�� | [2��+�ޣ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -4 | B�� | -2 | C�� | 4 | D�� | 2 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com