练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    2．已知ax≤xlnx-x+1对任意x∈[$\frac{1}{2}$，2]，恒成立，则a的最大值为（　　）
    A．0B．1C．2D．3

    分析 由题意ax≤xlnx-x+1对任意x∈[$\frac{1}{2}$，2]恒成立转化为a≤$\frac{xlnx-x+1}{x}$在[$\frac{1}{2}$，2]上恒成立即可；

    解答 解：由题意ax≤xlnx-x+1对任意x∈[$\frac{1}{2}$，2]恒成立即a≤$\frac{xlnx-x+1}{x}$在[$\frac{1}{2}$，2]上恒成立，
    令h（x）=$\frac{xlnx-x+1}{x}$=lnx+$\frac{1}{x}$-1；
    h'（x）=$\frac{1}{x}$-$\frac{1}{{x}^{2}}$，令h'（x）=0解得x=1；
    当x∈[$\frac{1}{2}$，1]时，h'（x）＜0，h（x）为单调减函数；
    当x∈[1，2]时，h'（x）＞0，h（x）为单调增函数；
    所以h（x）的最小值为h（1）=0
    所以，a的最大值为0；
    故选：A．

    点评 本题主要考查了函数转化思想，函数求值以及导函数与原函数的关系，属中等题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    12．{an}是各项均为正数的等差数列，{bn}是等比数列，已知$\frac{a_1}{b_1}$=$\frac{a_2}{b_2}$=1，$\frac{a_3}{b_3}$=$\frac{8}{9}$，那么$\frac{a_4}{b_4}$=（　　）
    A．$\frac{20}{27}$B．$\frac{16}{27}$C．$\frac{4}{9}$D．$\frac{20}{27}$或$\frac{16}{27}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

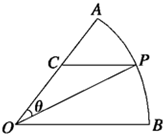    13．公园里有一扇形湖面，管理部门打算在湖中建一三角形观景平台，希望面积与周长都最大．如图所示扇形AOB，圆心角AOB的大小等于$\frac{π}{3}$，半径为2百米，在半径OA上取一点C，过点C作平行于OB的直线交弧AB于点P．设∠COP=θ；
    （1）求△POC面积S（θ）的函数表达式．
    （2）求S（θ）的最大值及此时θ的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．已知函数f（x）=alnx-ax（a≠0）．
    （I）讨论f（x）的单调性；
    （Ⅱ）若f（x）+（a+1）x+1-e≤0对任意x∈[e，e2]恒成立，求实数a的取值范围（e为自然常数）；
    （Ⅲ）求证lnn!≤$\frac{（n+2）（n-1）}{2}$（n≥2，n∈N*）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    17．某商场经营一批进价是30元/台的小商品，在市场试验中发现，此商品的销售单价x（x取整数）元与日销售量y台之间有如表关系：
    x35404550
    y56412811
    （1）画出散点图，并判断y与x是否具有线性相关关系？
    （2）求日销售量y对销售单价x的线性回归方程；
    （3）设经营此商品的日销售利润为P元，根据（1）写出P关于x的函数关系式，并预测当销售单价x为多少元时，才能获得最大日销售利润．（$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$，$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n（\overline{x}）^{2}}$）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．（1）若函数f（x）=$\frac{ax+1}{x+b}$的图象的对称中心为（2，1），求实数a、b．
    （2）已知函数y=f（x）的定义域为R，且当x∈R时，f（m+x）=-f（m-x）+2n恒成立，求证y=f（x）的图象关于点（m，n）对称．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．如图，在三棱柱ABC-A1B1C1中，E，F，G，H分别是AB，AC，A1B1，A1C1的中点，求证：
    （1）平面EFA1∥平面BCHG；
    （2）BG、CH、AA1三线共点．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．已知样本数据3，2，1，a的平均数为2，则样本的标准差是（　　）
    A．$\frac{\sqrt{2}}{2}$B．$\frac{\sqrt{3}}{3}$C．$\frac{1}{2}$D．$\frac{1}{4}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    12．已知sinα=$\frac{{2\sqrt{2}}}{3}$，cos（α+β）=-$\frac{1}{3}$，且α，β∈（0，$\frac{π}{2}$），则sin（α-β）的值等于$\frac{10\sqrt{2}}{27}$．

    查看答案和解析>>

    同步练习册答案