
分析 (Ⅰ)利用椭圆的离心率以及直线AF的斜率为$\sqrt{3}$,列出方程组求解a,b,即可的椭圆方程.
(Ⅱ)求出P(0,m),由$\overrightarrow{MP}$=λ$\overrightarrow{PN}$,得$\overrightarrow{OP}-\overrightarrow{OM}=λ(\overrightarrow{ON}-\overrightarrow{OP})$,转化求解λ,设M(x1,kx1+m),N(x2,kx2+m),联立直线与椭圆方程,利用判别式以及韦达定理得到k,m的不等式,通过向量关系求出k2=$\frac{4-{m}^{2}}{{m}^{2}-1}$.然后求解m的范围.
解答 解:(Ⅰ)由已知得$\left\{\begin{array}{l}{\frac{c}{a}=\frac{\sqrt{3}}{2}}\\{\frac{c}{b}=\sqrt{3}}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$,…(3分)
解得a=2,b=1.
∴椭圆E的方程为$\frac{{y}^{2}}{4}$+x2=1.…(5分)
(Ⅱ)根据已知得P(0,m),由$\overrightarrow{MP}$=λ$\overrightarrow{PN}$,得$\overrightarrow{OP}-\overrightarrow{OM}=λ(\overrightarrow{ON}-\overrightarrow{OP})$
∴$\overrightarrow{OM}+λ\overrightarrow{ON}=(1+λ)\overrightarrow{OP}$.
∵$\overrightarrow{OM}+λ\overrightarrow{ON}=4\overrightarrow{OP}$,∴(1+λ)$\overrightarrow{OP}$=$4\overrightarrow{OP}$.
∴1+λ=4,解得λ=3.…(7分)
设M(x1,kx1+m),N(x2,kx2+m),
由$\left\{\begin{array}{l}{y=kx+m}\\{4{x}^{2}+{y}^{2}-4=0}\end{array}\right.$,得(k2+4)x2+2mkx+m2-4=0(※)
由已知得△=4m2k2-4(k2+4)(m2-4)>0,即
k2-m2+4>0,
且x1+x2=$\frac{-2km}{{k}^{2}+4}$,x1x2=$\frac{{m}^{2}-4}{{k}^{2}+4}$.…(9分)
由$\overrightarrow{MP}=3\overrightarrow{PN}$,得-x1=3x2,即(x1+x2)+2x2=0.
∴x2=$\frac{km}{{k}^{2}+m}$.代入(※)式中整理得m2k2+m2-k2-4=0.…(10分)
当m2=1时,m2k2+m2-k2-4=0不成立.
∴k2=$\frac{4-{m}^{2}}{{m}^{2}-1}$.
∵k2-m2+4>0,
∴$\frac{4-{m}^{2}}{{m}^{2}-1}$-m2+4>0,即$\frac{(4-{m}^{2}){m}^{2}}{{m}^{2}-1}$>0.
∴1<m2<4,解得-2<m<-1或1<m<2.
综上所述,当-2<m<-1,或1<m<2时,$\overrightarrow{OM}+λ\overrightarrow{ON}=4\overrightarrow{OP}$.…(12分)
点评 本题考查直线与椭圆的位置关系的综合应用,有关范围的问题的解决方法,考查椭圆的求法,考查转化思想以及计算能力.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:高中数学 来源: 题型:填空题
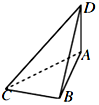 如图,在正三棱柱ABC-A1B1C1中,D为棱AA1的中点.若截面△BC1D是面积为6的直角三角形,则此三棱柱的体积为$8\sqrt{3}$.
如图,在正三棱柱ABC-A1B1C1中,D为棱AA1的中点.若截面△BC1D是面积为6的直角三角形,则此三棱柱的体积为$8\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({kπ-\frac{π}{2},kπ+\frac{π}{2}})({k∈Z})$ | B. | (kπ,kπ+π)(k∈Z) | C. | $({kπ-\frac{3π}{4},kπ+\frac{π}{4}})({k∈Z})$ | D. | $({kπ-\frac{π}{4},kπ+\frac{3π}{4}})({k∈Z})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①③ | B. | ②③ | C. | ③④ | D. | ①③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 12 | B. | 8 | C. | 4 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com