
分析 分别求出p,q为真时的a的范围,通过讨论p,q的真假,求出a的范围即可.
解答 解:若p是真命题,则△=(2a)2-4a≤0,解得:0≤a≤1,
若q是真命题,则$\left\{\begin{array}{l}{x-4y-a=0}\\{{x}^{2}=4y}\end{array}\right.$,得:x2-x+a=0有实数解,
∴△=(-1)2-4a≥0,解得:a≤$\frac{1}{4}$,
由¬(p∨q)”为假命题,“p∧q”为假命题,
得p,q一真一假,
p真q假时,$\frac{1}{4}$<a≤1,
p假q真时,a<0,
综上,a∈(-∞,0)∪($\frac{1}{4}$,1].
点评 本题考查了复合命题的判断,考查函数恒成立问题,考查直线和抛物线的关系,是一道中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4,1 | B. | 3,2 | C. | 4,2 | D. | 3,1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
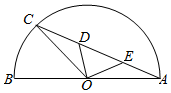 如图,$\widehat{AB}$为半圆,O为圆心,OA=1,C为$\widehat{AB}$上的动点,D、E为线段AC的三等分点,设∠AOC=α,将△ODE的面积为y=f(α),则y=f(α)的图象大致为( )
如图,$\widehat{AB}$为半圆,O为圆心,OA=1,C为$\widehat{AB}$上的动点,D、E为线段AC的三等分点,设∠AOC=α,将△ODE的面积为y=f(α),则y=f(α)的图象大致为( )| A. | 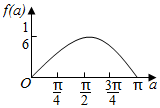 | B. |  | ||
| C. | 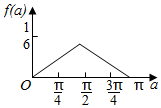 | D. | 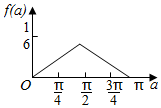 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com