
分析 根据题意分类讨论即可求出.
解答 解:①当k<0时,则x>0,即不等式的解集为{x|x>0},
②当k=0时,x≠1,即不等式的解集为{x|x≠1},
③当k>0时,则x<0,即不等式的解集为{x|x<0},
④当k>0,x>0时,
则|1-x|>k2x2,
1°当x≥1时,即x-1>k2x2,即k2x2-x+1<0,
当△<0时,即1-4k2<0时,即k>$\frac{1}{2}$时,不等式的解集为空集,
当△≥0时,即1-4k2≥0时,即0<k≤$\frac{1}{2}$时,则$\frac{1-\sqrt{1-4{k}^{2}}}{2{k}^{2}}$<x<$\frac{1+\sqrt{1-4{k}^{2}}}{2{k}^{2}}$,因为$\frac{1+\sqrt{1-4{k}^{2}}}{2{k}^{2}}$>1,
即不等式的解集为{x|1≤x<$\frac{1+\sqrt{1-4{k}^{2}}}{2{k}^{2}}$},
2°当0<x<1时,即1-x>k2x2,即k2x2+x-1<0,
△=1+4k2>0时,则$\frac{-1+\sqrt{1+4{k}^{2}}}{2{k}^{2}}$<x<1,即不等式的解集为{x|0<x<$\frac{-1+\sqrt{1+4{k}^{2}}}{2{k}^{2}}$},
⑤当k<0,x<0时,即1-x>k2x2,即k2x2+x-1<0,
△=1+4k2>0时,则$\frac{-1-\sqrt{1+4{k}^{2}}}{2{k}^{2}}$<x<$\frac{-1+\sqrt{1+4{k}^{2}}}{2{k}^{2}}$,即不等式的解集为{x|$\frac{-1-\sqrt{1+4{k}^{2}}}{2{k}^{2}}$<x<0}.
⑥当x=0时,不等式对于k取任何数都成立,
综上所述,当k<0时,不等式的解集为{x|x>$\frac{-1-\sqrt{1+4{k}^{2}}}{2{k}^{2}}$}.
当k=0时,不等式的解集为{x|x≠1},
当0<k≤$\frac{1}{2}$时,不等式的解集为{x|x|1≤x<$\frac{1+\sqrt{1-4{k}^{2}}}{2{k}^{2}}$},
当k>$\frac{1}{2}$时,不等式的解集为{x|x=0}.
点评 本题考查了不等式的解法,关键是分类讨论,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
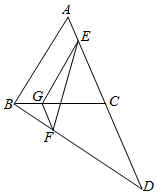 如图,AB、CD是两条异面直线,AB=CD=3,E、F分别是AC、BD上的点,且AE:EC=BF:DF=1:2,EF=$\sqrt{7}$,求AB和CD所成角的大小.
如图,AB、CD是两条异面直线,AB=CD=3,E、F分别是AC、BD上的点,且AE:EC=BF:DF=1:2,EF=$\sqrt{7}$,求AB和CD所成角的大小.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
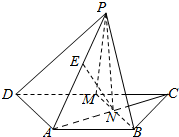 如图.已知等腰梯形ABCD中,AB∥CD,AD=AB=$\frac{1}{2}$CD,M是的CD的中点.N是AC与BM的交点,将△BCM沿BM向上翻折成△BPM,使平面BPM⊥平面ABMD
如图.已知等腰梯形ABCD中,AB∥CD,AD=AB=$\frac{1}{2}$CD,M是的CD的中点.N是AC与BM的交点,将△BCM沿BM向上翻折成△BPM,使平面BPM⊥平面ABMD查看答案和解析>>
科目:高中数学 来源: 题型:填空题
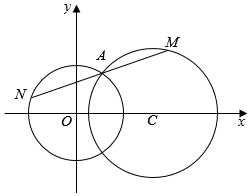 如图,已知点A为圆O:x2+y2=9与圆C:(x-5)2+y2=16在第一象限内的交点.过A的直线1被圆O和圆C所截得的弦分别为NA,MA(M,N不重合).若|NA|=|MA|,则直线1的方程是7x-24y+45=0.
如图,已知点A为圆O:x2+y2=9与圆C:(x-5)2+y2=16在第一象限内的交点.过A的直线1被圆O和圆C所截得的弦分别为NA,MA(M,N不重合).若|NA|=|MA|,则直线1的方程是7x-24y+45=0.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com