
分析 分m>n和m<n两种情况分析,对于每一种情况,由椭圆方程求出焦距,设出P的坐标,由三角形面积公式求得面积,得到P的纵坐标(或横坐标),把使△PF1F2的面积等于n2的点P恰有4个转化为P的坐标与短半轴间的关系,由此求出n的范围,利用几何概型求概率.
解答 解:当m>n时,a2=m2,b2=n2,
∴c2=a2-b2=m2-n2,$c=\sqrt{{m}^{2}-{n}^{2}}$,
设P(xP,yP),
则${S}_{△P{F}_{1}{F}_{2}}=\frac{1}{2}×2\sqrt{{m}^{2}-{n}^{2}}×|{y}_{P}|$=n2,
∴$|{y}_{P}|=\frac{{n}^{2}}{\sqrt{{m}^{2}-{n}^{2}}}$,
若使△PF1F2的面积等于n2的点P恰有4个,
则$|{y}_{P}|=\frac{{n}^{2}}{\sqrt{{m}^{2}-{n}^{2}}}$<n,即n2<m2-n2,
∴2n2<m2,
∵m2<1,∴2n2<1,则-$\frac{\sqrt{2}}{2}<n<\frac{\sqrt{2}}{2}$,
又0<n<1,则0$<n<\frac{\sqrt{2}}{2}$,
由几何概型可得,使△PF1F2的面积等于n2的点P恰有4个的概率是$\frac{\sqrt{2}}{2}$;
当m<n时,a2=n2,b2=m2,
∴c2=a2-b2=n2-m2,$c=\sqrt{{n}^{2}-{m}^{2}}$,
设P(xP,yP),
则${S}_{△P{F}_{1}{F}_{2}}=\frac{1}{2}×2×\sqrt{{n}^{2}-{m}^{2}}×|{x}_{P}|={n}^{2}$,
∴$|{x}_{P}|=\frac{{n}^{2}}{\sqrt{{n}^{2}-{m}^{2}}}<m$,即$(\frac{{m}^{2}}{{n}^{2}})^{2}-\frac{{m}^{2}}{{n}^{2}}+1<0$,
此时$\frac{m}{n}$无解,即使△PF1F2的面积等于n2的点P恰有4个的概率是0.
综上,使△PF1F2的面积等于n2的点P恰有4个的概率是$\frac{\sqrt{2}}{2}$或0.
故答案为:$\frac{\sqrt{2}}{2}$或0.
点评 本题考查椭圆的简单性质,考查了与焦点三角形有关的面积问题,考查几何概型的应用,体现了数学转化思想方法,有一定难度.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
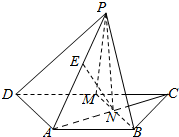 如图.已知等腰梯形ABCD中,AB∥CD,AD=AB=$\frac{1}{2}$CD,M是的CD的中点.N是AC与BM的交点,将△BCM沿BM向上翻折成△BPM,使平面BPM⊥平面ABMD
如图.已知等腰梯形ABCD中,AB∥CD,AD=AB=$\frac{1}{2}$CD,M是的CD的中点.N是AC与BM的交点,将△BCM沿BM向上翻折成△BPM,使平面BPM⊥平面ABMD查看答案和解析>>
科目:高中数学 来源: 题型:填空题
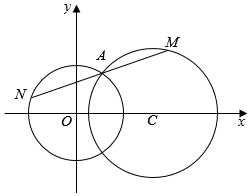 如图,已知点A为圆O:x2+y2=9与圆C:(x-5)2+y2=16在第一象限内的交点.过A的直线1被圆O和圆C所截得的弦分别为NA,MA(M,N不重合).若|NA|=|MA|,则直线1的方程是7x-24y+45=0.
如图,已知点A为圆O:x2+y2=9与圆C:(x-5)2+y2=16在第一象限内的交点.过A的直线1被圆O和圆C所截得的弦分别为NA,MA(M,N不重合).若|NA|=|MA|,则直线1的方程是7x-24y+45=0.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | $\frac{18}{4a+1}$ | ||
| C. | $\frac{18}{a+4}$或$\frac{18}{4a+1}$ | D. | $\frac{18}{4a+1}$或$\frac{18}{a+4}$或$\frac{9\sqrt{a}}{2a}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com