
���� ����������ɵ�����{$log_2^{\;}{a_n}$}������Ϊ$log_2^{\;}{a_1}=log_2^{\;}2=1$������Ϊ1�ĵȲ����У������������{an}��ͨ�ʽ��
�������ô�λ����������������{cn}��ǰn���Tn��
�����������{bn}��ͨ����õ�b1��bm��bn�ɵȱ����У�������m��n��1��m��n�������ɵó����ۣ�
��� �⣺���߶������n��N*��n��2��$log_2^{\;}{a_n}=1+log_2^{\;}{a_{n-1}}$��
����$log_2^{\;}{a_n}-log_2^{\;}{a_{n-1}}=1$
������{$log_2^{\;}{a_n}$}������Ϊ$log_2^{\;}{a_1}=log_2^{\;}2=1$������Ϊ1�ĵȲ����У�
��$log_2^{\;}{a_n}=1+1����n-1��=n$��
��an=2n����n��N*��
������cn=��3n-1��•an=��3n-1����2n��
��${T_n}=2��{2^1}+5��{2^2}+8��{2^3}+��+��{3n-4}����{2^{n-1}}+��{3n-1}����{2^n}$��
��$2{T_n}=2��{2^2}+5��{2^3}+8��{2^4}+��+��{3n-4}����{2^n}+��{3n-1}����{2^{n+1}}$��
��$-{T_n}=2��{2^1}+3��{2^2}+3��{2^3}+��+3��{2^{n-1}}+3��{2^n}-��{3n-1}����{2^{n+1}}$��
��$-{T_n}=6��\frac{{{2^n}-1}}{2-1}-2-��{3n-1}����{2^{n+1}}=-��6n-8��•{2^n}-8$
��${T_n}=��6n-8��•{2^n}+8$
����bn=$\frac{{na_n^{\;}}}{{��2n+1��•{2^n}}}$=$\frac{n}{2n+1}$����b1��bm��bn�ɵȱ����У�
��$\frac{m}{2m+1}$��2=$\frac{1}{3}$��$\frac{n}{2n+1}$������$\frac{{m}^{2}}{4{m}^{2}+4m+1}$=$\frac{n}{6n+3}$��
�ɵ�$\frac{3}{n}$=$\frac{-2{m}^{2}+4m+1}{{m}^{2}}$��
����-2m2+4m+1��0����ã�1-$\frac{\sqrt{6}}{2}$��m��1+$\frac{\sqrt{6}}{2}$��
��m��n��N*����m��1��
��m=2����ʱn=12����
�ʵ��ҽ���m=2����2��ʹ��b1��bm��bn�ɵȱ����У�
���� ���⿼�����е���ʽ������ȱ����е�֤�����������е�ͨ���Լ���λ�������ͣ���ȷ�������е���ʽ�ǹؼ��������е��⣮


 �¿α�����Ķ�ѵ��ϵ�д�
�¿α�����Ķ�ѵ��ϵ�д� ������������Ӧ����ϵ�д�
������������Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{2}$ | B�� | 1 | C�� | $\frac{3}{2}$ | D�� | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\vec a$-$\vec b$ | B�� | $\vec b$-$\vec a$ | C�� | $\frac{1}{2}$��$\vec a$-$\vec b$�� | D�� | $\frac{1}{2}$��$\vec b$-$\vec a$�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
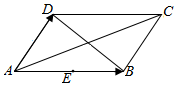
| A�� | $\overrightarrow{AC}$=$\overrightarrow a$+$\overrightarrow b$ | B�� | $\overrightarrow{BD}$=$\overrightarrow a$-$\overrightarrow b$ | C�� | $\overrightarrow{AE}$=$\frac{1}{2}$$\overrightarrow a$ | D�� | $\overrightarrow{CB}$=-$\overrightarrow b$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | {x|0��x��3} | B�� | {x|-3��x��3} | C�� | {0��1��2} | D�� | {0��1��3} |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��һ���� | B�� | �ڶ����� | C�� | �������� | D�� | �������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-1��3�� | B�� | ��1��3�� | C�� | ��3��+�ޣ� | D�� | ��1��3���ȣ�3��+�ޣ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com