
在 中,角A、B、C的对边分别为
中,角A、B、C的对边分别为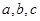 ,已知向量
,已知向量 ,
, ,且
,且 。
。
(1)求角 的大小;
的大小;
(2)若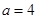 ,求
,求 面积的最大值。(12分)
面积的最大值。(12分)
科目:高中数学 来源: 题型:解答题
已知△ABC的内角A,B,C所对的边分别是a,b,c,设向量m=(a,b),n=(sin B,sin A),p=(b-2,a-2).
(1)若m∥n,求证:△ABC为等腰三角形;
(2)若m⊥p,边长c=2,C= ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,在海岸线一侧C处有一个美丽的小岛,某旅游公司为方便游客,在上设立了A、B两个报名点,满足A、B、C中任意两点间的距离为10千米。公司拟按以下思路运作:先将A、B两处游客分别乘车集中到AB之间的中转点D处(点D异于A、B两点),然后乘同一艘游轮前往C岛。据统计,每批游客A处需发车2辆,B处需发车4辆,每辆汽车每千米耗费2元,游轮每千米耗费12元。设∠ ,每批游客从各自报名点到C岛所需运输成本S元。
,每批游客从各自报名点到C岛所需运输成本S元。
⑴写出S关于 的函数表达式,并指出
的函数表达式,并指出 的取值范围;
的取值范围;
⑵问中转点D距离A处多远时,S最小?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com