Question

1．甲、乙，丙3个盒中分别装有大小相等，形状相同的卡片若干张，甲盒中装有2张卡片，分别写有字母A和B；乙盒中装有3张卡片，分别写有字母C，D和E；丙盒中装有2张卡片，分别写有字母H和I，现要从3个盒中各随机取出1张卡片．求：（1）取出的3张卡片中恰好有1张、2张、3张写有元音字母的概率各是多少；
（2）取出的3张卡片上全是辅音字母的概率．

Answer 1

分析 （1）作出树形图，由树形图，得所有可能出现的结果有12个，利用列举法能求出取出的3张卡片中恰好有1张、2张、3张写有元音字母的概率各是多少．
（2）满足全是辅音字母的结果有2个，由此能求出取出的3张卡片上全是辅音字母的概率．

解答 解：（1）作出树形图，如下：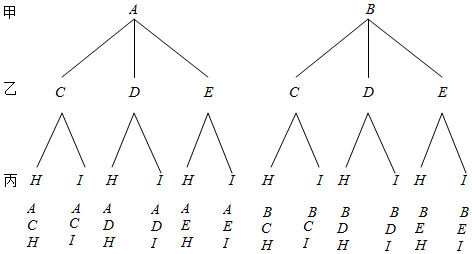

由树形图，得所有可能出现的结果有12个，它们出现的可能性相等，
其中满足只有一个元音字母的结果有5个，
∴取出的3张卡片中恰好有1张写有元音字母的概率p₁=$\frac{5}{12}$；
其中满足只有两个元音字母的结果有4个，
∴取出的3张卡片中恰好有2张写有元音字母的概率p₂=$\frac{4}{12}=\frac{1}{3}$；
其中满足三个元音字母的结果有1个，
∴取出的3张卡片中都写有元音字母的概率p₃=$\frac{1}{12}$．
（2）满足全是辅音字母的结果有2个，
则取出的3张卡片上全是辅音字母的概率p=$\frac{2}{12}=\frac{1}{6}$．

点评 本题考查概率的求法，是基础题，解题时要认真审题，注意等可能事件概率计算公式的合理运用．