
【题目】在矩形ABCD中,AB=1,AD=2,动点P在以点C为圆心且与BD相切的圆上.若![]() =λ
=λ![]() +μ
+μ![]() ,则λ+μ的最大值为( )
,则λ+μ的最大值为( )
A. 3 B. 2![]()
C. ![]() D. 2
D. 2
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:高中数学 来源: 题型:
【题目】经过长期观测得到:在交通繁忙的时段,某公路段的车流量![]() (千辆/小时)与汽车的平均速度
(千辆/小时)与汽车的平均速度![]() (千米/小时)之间的函数关系为:
(千米/小时)之间的函数关系为:![]() .
.
(1)在该时段内,当汽车的平均速度![]() 为多少时,车流量最大?最大车流量为多少?
为多少时,车流量最大?最大车流量为多少?
(2)若要求在该时段内车流量超过10千辆/小时,则汽车的平均速度应在什么范围?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着网络的发展,网上购物越来越受到人们的喜爱,各大购物网站为增加收入,促销策略越来越多样化,促销费用也不断增加.下表是某购物网站2017年1-8月促销费用(万元)和产品销量(万件)的具体数据.

(1)根据数据可知![]() 与
与![]() 具有线性相关关系,请建立
具有线性相关关系,请建立![]() 关于
关于![]() 的回归方程
的回归方程![]() (系数精确到
(系数精确到![]() );
);
(2)已知6月份该购物网站为庆祝成立1周年,特制定奖励制度:以![]() (单位:件)表示日销量,
(单位:件)表示日销量, ![]() ,则每位员工每日奖励100元;
,则每位员工每日奖励100元; ![]() ,则每位员工每日奖励150元;
,则每位员工每日奖励150元; ![]() ,则每位员工每日奖励200元.现已知该网站6月份日销量
,则每位员工每日奖励200元.现已知该网站6月份日销量![]() 服从正态分布
服从正态分布![]() ,请你计算某位员工当月奖励金额总数大约多少元.(当月奖励金额总数精确到百分位)
,请你计算某位员工当月奖励金额总数大约多少元.(当月奖励金额总数精确到百分位)
参考数据: ![]() ,
, ![]() ,其中
,其中![]() ,
, ![]() 分别为第
分别为第![]() 个月的促销费用和产品销量,
个月的促销费用和产品销量, ![]() .
.
参考公式:
(1)对于一组数据![]() ,
, ![]() ,
, ![]() ,
, ![]() ,其回归方程
,其回归方程![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为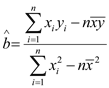 ,
, ![]() .
.
(2)若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在图所示的五面体中,面ABCD为直角梯形,![]() ,平面
,平面![]() 平面ABCD,
平面ABCD,![]() ,
,![]() ,
,![]() 是边长为2的正三角形.
是边长为2的正三角形.

![]() 证明:
证明:![]() 平面ACF;
平面ACF;
![]() 若点P在线段EF上,且二面角
若点P在线段EF上,且二面角![]() 的余弦值为
的余弦值为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() (k为常数,e=2.718 28…是自然对数的底数).
(k为常数,e=2.718 28…是自然对数的底数).
(1)当k≤0时,求函数f (x)的单调区间;
(2)若函数f (x)在(0,2)内存在两个极值点,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的几何体中,四边形![]() 为正方形,四边形
为正方形,四边形![]() 为直角梯形,且
为直角梯形,且![]() ,
, ![]() ,平面
,平面![]() 平面
平面![]() ,
, ![]() .
.

(![]() )求证:
)求证: ![]() 平面
平面![]() .
.
(![]() )若二面角
)若二面角![]() 为直二面角,
为直二面角,
(i)求直线![]() 与平面
与平面![]() 所成角的大小.
所成角的大小.
(ii)棱![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an} 和等比数列{bn}满足a1=b1=1,a2+a4=10,b2b4=a5.
(1)求{an}的通项公式;
(2)求和:b1+b3+b5+…+b2n-1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中文“函数”(function)一词,最早由近代数学家李善兰翻译的之所以这么翻译,他给出的原因是“凡此变数中函彼变数者,则此为彼之函数”,也即函数指一个量随着另一个量的变化而变化下列选项中两个函数相等的是( )
A.![]() 与
与![]() B.
B.![]() 与
与![]()
C.![]() 与
与![]() D.
D.![]() 与
与![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com