
分析 (Ⅰ)求当a=2时,函数的导数,求得切线的斜率和切点,由点斜式方程即可得到切线方程;
(Ⅱ)问题转化为b=x2-3x+lnx有唯一实数解,(x>0),令g(x)=x2-3x+lnx,(x>0),根据函数的单调性求出g(x)的极值,从而求出b的范围即可;
(Ⅲ)函数f(x)在(0,+∞)上有两个极值点,可得0<a<$\frac{1}{2}$,不等式f(x1)≥mx2恒成立即为 $\frac{f{(x}_{1})}{{x}_{2}}$≥m,求得 $\frac{f{(x}_{1})}{{x}_{2}}$=1-x1+$\frac{1}{{x}_{1}-1}$+2x1lnx1,令h(x)=1-x+$\frac{1}{x-1}$+2xlnx(0<x<$\frac{1}{2}$),求出导数,判断单调性,即可得到h(x)的范围,即可求得m的范围.
解答 解:(Ⅰ)当a=2时,f(x)=x2-2x+2lnx,f′(x)=2x-2+$\frac{2}{x}$,
则f(1)=-1,f'(1)=2,
所以切线方程为y+1=2(x-1),
即为y=2x-3.
(Ⅱ)a=1时,f(x)=x2-2x+lnx,(x>0),
若关于x的方程f(x)=x+b有唯一实数解,
即b=x2-3x+lnx有唯一实数解,(x>0),
令g(x)=x2-3x+lnx,(x>0),
则g′(x)=2x-3+$\frac{1}{x}$=$\frac{{2x}^{2}-3x+1}{x}$=$\frac{(2x-1)(x-1)}{x}$,
令g′(x)>0,解得:x>1或0<x<$\frac{1}{2}$,
令g′(x)<0,解得:$\frac{1}{2}$<x<1,
故g(x)在(0,$\frac{1}{2}$)递增,在($\frac{1}{2}$,1)递减,在(1,+∞)递增,
故g(x)极大值=g($\frac{1}{2}$)=-$\frac{5}{4}$-ln2,g(x)极小值=g(1)═-2,
故b>-$\frac{5}{4}$-ln2,或b<-2;
(Ⅲ)f′(x)=2x-2+$\frac{a}{x}$=$\frac{{2x}^{2}-2x+a}{x}$(x>0),
令f'(x)=0,得2x2-2x+a=0,
当△=4-8a>0且a>0,即0<a<$\frac{1}{2}$时,由2x2-2x+a=0,得x1,2=$\frac{1±\sqrt{1-2a}}{2}$,
由f'(x)>0,得0<x<$\frac{1-\sqrt{1-2a}}{2}$或x>$\frac{1+\sqrt{1-2a}}{2}$;
由f'(x)<0,得 $\frac{1-\sqrt{1-2a}}{2}$<x<$\frac{1+\sqrt{1-2a}}{2}$,
故若函数f(x)在(0,+∞)上有两个极值点,可得0<a<$\frac{1}{2}$,
由f'(x)=0,得2x2-2x+a=0,则x1+x2=1,x1=$\frac{1-\sqrt{1-2a}}{2}$,x2=$\frac{1+\sqrt{1-2a}}{2}$,
由0<a<$\frac{1}{2}$,可得0<x1<$\frac{1}{2}$,$\frac{1}{2}$<x2<1,
$\frac{f{(x}_{1})}{{x}_{2}}$=$\frac{{{x}_{1}}^{2}-{2x}_{1}+al{nx}_{1}}{{x}_{2}}$=$\frac{{{x}_{1}}^{2}-{2x}_{1}+({2x}_{1}-{{2x}_{1}}^{2})l{nx}_{1}}{1{-x}_{1}}$
=1-x1+$\frac{1}{{x}_{1}-1}$+2x1lnx1,
令h(x)=1-x+$\frac{1}{x-1}$+2xlnx(0<x<$\frac{1}{2}$),
h′(x)=-1-$\frac{1}{{(x-1)}^{2}}$+2lnx,
由0<x<$\frac{1}{2}$,则-1<x-1<-$\frac{1}{2}$,$\frac{1}{4}$<(x-1)2<1,-4<-$\frac{1}{{(x-1)}^{2}}$<-1,
又2lnx<0,则h′(x)<0,即h(x)在(0,$\frac{1}{2}$)递减,
即有h(x)>h($\frac{1}{2}$)=-$\frac{3}{2}$-ln2,即 $\frac{f(x)}{x}$>-$\frac{3}{2}$-ln2,
即有实数m的取值范围为(-∞,-$\frac{3}{2}$-ln2].
点评 本题考查导数的运用:求切线方程和单调区间、极值,主要考查导数的几何意义,同时考查函数的单调性的运用,以及不等式恒成立问题转化为求函数的最值或范围,属于综合题.


科目:高中数学 来源:2017届湖南长沙长郡中学高三上周测十二数学(理)试卷(解析版) 题型:解答题
在一个盒子里装有6张卡片,上面分别写着如下定义域为 的函数:
的函数:
 ,
,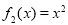 ,
,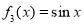 ,
,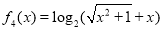 ,
, ,
,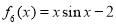 .
.
(1)现在从盒子中任意取两张卡片,记事件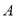 为“这两张卡片上函数相加,所得新函数是奇函数”,求事件
为“这两张卡片上函数相加,所得新函数是奇函数”,求事件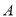 的概率;
的概率;
(2)从盒中不放回逐一抽取卡片,若取到一张卡片上的函数是偶函数则停止抽取,否则继续进行,记停止时抽取次数为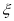 ,写出
,写出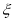 的分布列,并求其数学期望
的分布列,并求其数学期望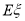 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图给出的是计算1+$\frac{1}{3}$+$\frac{1}{5}$+…+$\frac{1}{2017}$的值的一个程序框图,则判断框内应填入的条件是( )
如图给出的是计算1+$\frac{1}{3}$+$\frac{1}{5}$+…+$\frac{1}{2017}$的值的一个程序框图,则判断框内应填入的条件是( )| A. | i≤1009 | B. | i>1009 | C. | i≤1010 | D. | i>1010 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
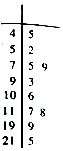 空气质量指数(Air Quality Index,简称AQI)是定量描述空气质量状况的无量纲指数,参与空气质量评价的主要污染物为SO2、NO2、PM10、PM2.5、O3、CO等六项.空气质量按照AQI大小分为六级:一级0~50为优;二级51~100为良好;三级101~150为轻度污染;四级151~200为中度污染;五级201~300为重度污染;六级>300为严重污染.
空气质量指数(Air Quality Index,简称AQI)是定量描述空气质量状况的无量纲指数,参与空气质量评价的主要污染物为SO2、NO2、PM10、PM2.5、O3、CO等六项.空气质量按照AQI大小分为六级:一级0~50为优;二级51~100为良好;三级101~150为轻度污染;四级151~200为中度污染;五级201~300为重度污染;六级>300为严重污染.查看答案和解析>>
科目:高中数学 来源:2017届湖南长沙长郡中学高三上周测十二数学(理)试卷(解析版) 题型:填空题
若数列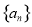 满足
满足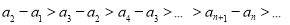 ,则称数列
,则称数列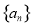 为“差递减”数列.若数列
为“差递减”数列.若数列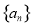 是“差递减”数列,且其通项
是“差递减”数列,且其通项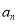 与其前
与其前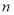 项和
项和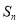 (
( )满足
)满足 (
( ),则实数
),则实数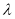 的取值范围是 .
的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2017届湖南长沙长郡中学高三上周测十二数学(理)试卷(解析版) 题型:填空题
已知点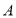 、
、 分别是椭圆
分别是椭圆 :
: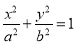 (
( )的上顶点和左焦点,若
)的上顶点和左焦点,若 于圆
于圆 :
: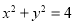 相切于点
相切于点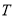 ,且点
,且点 是线段
是线段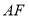 靠近点
靠近点 的三等分点,则椭圆
的三等分点,则椭圆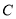 的标准方程为 .
的标准方程为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com