
分析 (1)由柯西不等式可得:($\sqrt{a}$+$\sqrt{b}$+$\sqrt{c}$)2≤(a+b+c)(1+1+1),代入条件,即可证明结论;
(2)利用综合法,由a+b+c=1⇒a2+b2+c2+2ab+2bc+2ac,利用重要不等式a2+b2≥2ab,a2+c2≥2ac,b2+c2≥2bc,易证a2+b2+c2≥ab+bc+ac,与前者联立可证得结论.
解答 证明:(1)由柯西不等式可得:($\sqrt{a}$+$\sqrt{b}$+$\sqrt{c}$)2≤(a+b+c)(1+1+1),
∵a+b+c=1,
∴($\sqrt{a}$+$\sqrt{b}$+$\sqrt{c}$)2≤3,
∴$\sqrt{a}$+$\sqrt{b}$+$\sqrt{c}$≤$\sqrt{3}$;
(2)∵a+b+c=1,
∴a2+b2+c2+2ab+2bc+2ac,
又a2+b2≥2ab,a2+c2≥2ac,b2+c2≥2bc,
将以上三个不等式相加得:2(a2+b2+c2)≥(2ab+2bc+2ac),
即a2+b2+c2≥ab+bc+ac,
∴1=a2+b2+c2+2ab+2bc+2ac≥ab+bc+ac+2ab+2bc+2ac=3(ab+bc+ac),
∴ab+bc+ca≤$\frac{1}{3}$.
点评 本题考查不等式的证明,着重考查综合法的运用,考查推理论证能力,属于中档题.


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 一条折线段 | B. | 一条线段 | C. | 一段圆弧 | D. | 一段抛物线 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
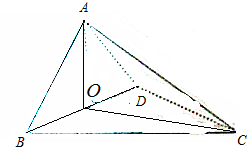 如图,四面体ABCD中,O是BD的中点,△ABD和△BCD均为等边三角形,AB=2,AC=$\sqrt{6}$.
如图,四面体ABCD中,O是BD的中点,△ABD和△BCD均为等边三角形,AB=2,AC=$\sqrt{6}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com