
(本题10分)某校高三某班的一次数学测试成绩(满分为100分)的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如下,据此解答如下问题:
(1)求分数在[50,60)的频率及全班人数;(2)求分数在[80,90)之间的频数,并计算频率分布直方图中[80,90)间的矩形的高;(3)若要从分数在[80,100]之间的试卷中任取两份分析学生失分情况,在抽取的试卷中,求分数在[90,100]之间的份数 的数学期望
的数学期望 .
.
(1)25;(2)频数为4,频率0.016;(3) 。
。
解析试题分析:(1)分数在[50,60)的频率为0.008×10=0.08,由茎叶图知:分数在[50,60)之间的频数为2,所以全班人数为 =25, ┄┄┄┄2分
=25, ┄┄┄┄2分
(2)分数在[80,90)之间的频数为25-2-7-10-2=4;
频率分布直方图中[80,90)间的矩形的高为 ÷10=0.016. ┄┄┄┄ 5分
÷10=0.016. ┄┄┄┄ 5分
(3)由(2)知分数在[80,90)之间的人数为4,由茎叶图可知分数在[90,100]之间的人数为2 , 的可能取值为0,1,2.
的可能取值为0,1,2.  ,
, ┄┄┄┄8分
┄┄┄┄8分
随机变量 的分布列为
的分布列为
数学期望 . ┄┄┄┄ 10分
. ┄┄┄┄ 10分
考点:频率分布直方图;茎叶图;等可能事件的概率;数学期望。
点评:本题主要考查频率分步直方图和等可能事件的概率,本题是一个基础题.


科目:高中数学 来源: 题型:解答题
某学生参加某高校的自主招生考试,须依次参加A、B、C、D、E五项考试,如果前四项中有两项不合格或第五项不合格,则该考生就被淘汰,考试即结束;考生未被淘汰时,一定继续参加后面的考试。已知每一项测试都是相互独立的,该生参加A、B、C、D四项考试不合格的概率均为 ,参加第五项不合格的概率为
,参加第五项不合格的概率为
(1)求该生被录取的概率;
(2)记该生参加考试的项数为 ,求
,求 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
为了解社会对学校办学质量的满意程度,某学校决定用分层抽样的方法从高中三个年级的家长委员会中共抽取6人进行问卷调查,已知高一、高二、高三的家长委员会分别有54人、1 8人、36人.
(I)求从三个年级的家长委员会中分别应抽的家长人数;
(Ⅱ)若从抽得的6人中随机抽取2人进行训查结果的对比,求这2人中至少有一人是高三学生家长的慨率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)盒中有大小相同的编号为1,2,3,4,5,6的六只小球,规定:从盒中一次摸出'2只球,如果这2只球的编号均能被3整除,则获一等奖,奖金10元,如果这2只球的编号均为偶数,则获二等奖,奖金2元,其他情况均不获奖.
(1)若某人参加摸球游戏一次获奖金x元,求x的分布列及期望;
(2)若某人摸一次且获奖,求他获得一等奖的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某机构向民间招募防爆犬,首先进行入围测试,计划考察三个项目:体能,嗅觉和反应.这三个项目中只要有两个通过测试,就可以入围.某训犬基地有4只优质犬参加测试,已知它们通过体能测试的概率都是1/3,通过嗅觉测试的概率都是1/3,通过反应测试的概率都是1/2.
求(1)每只优质犬能够入围的概率;
(2)若每入围1只犬给基地记10分,设基地的得分为随机变量ξ,求ξ的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)为了参加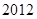 年贵州省高中篮球比赛,某中学决定从四个篮球较强的班级中选出
年贵州省高中篮球比赛,某中学决定从四个篮球较强的班级中选出 人组成男子篮球队代表所在地区参赛,队员来源人数如下表:
人组成男子篮球队代表所在地区参赛,队员来源人数如下表:
| 班级 | 高三(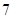 )班 )班 | 高三(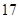 )班 )班 | 高二( )班 )班 | 高二(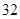 )班 )班 |
| 人数 |  | 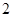 |  |  |
 名队员中随机选出两名,求两人来自同一班级的概率;(II)该中学篮球队经过奋力拼搏获得冠军.若要求选出两位队员代表冠军队发言,设其中来自高三(7)班的人数为
名队员中随机选出两名,求两人来自同一班级的概率;(II)该中学篮球队经过奋力拼搏获得冠军.若要求选出两位队员代表冠军队发言,设其中来自高三(7)班的人数为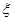 ,求随机变量
,求随机变量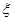 的分布列及数学期望
的分布列及数学期望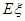 .
.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分12分)
已知关于x的二次函数
(1)设集合 和
和 ,从集合
,从集合 中随机取一个数作为
中随机取一个数作为 ,从
,从 中随机取一个数作为
中随机取一个数作为 ,求函数
,求函数 在区间
在区间 上是增函数的概率;
上是增函数的概率;
(2)设点 是区域
是区域 内的随机点,求函数
内的随机点,求函数 在区间
在区间 上是增函数的概率。
上是增函数的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
甲,乙两人进行乒乓球比赛,约定每局胜者得 分,负者得
分,负者得 分,比赛进行到有一人比对方多
分,比赛进行到有一人比对方多 分或打满
分或打满 局时停止.设甲在每局中获胜的概率为
局时停止.设甲在每局中获胜的概率为 ,且各局胜负相互独立.若第二局比赛结束时比赛停止的概率为
,且各局胜负相互独立.若第二局比赛结束时比赛停止的概率为 .
.
(1)求 的值;
的值;
(2)设 表示比赛停止时比赛的局数,求随机变量
表示比赛停止时比赛的局数,求随机变量 的分布列和数学期望
的分布列和数学期望 。
。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
甲乙两名射手互不影响地进行射击训练,根据以往的数据统计,他们设计成绩的分布列如下:
| 射手甲 | 射手乙 | ||||||
| 环数 | 8 | 9 | 10 | 环数 | 8 | 9 | 10 |
| 概率 |  |  |  | 概率 |  |  |  |
 ,求
,求 的分布列和期望.
的分布列和期望. 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com