
【题目】(1)利用“五点法”画出函数![]() 在长度为一个周期的闭区间的简图.
在长度为一个周期的闭区间的简图.
列表:
| |||||
x | |||||
y |
作图:
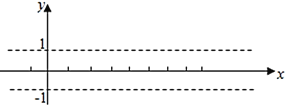
(2)并说明该函数图象可由![]() 的图象经过怎么变换得到的.
的图象经过怎么变换得到的.
(3)求函数![]() 图象的对称轴方程.
图象的对称轴方程.
 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:
【题目】已知点![]() ,过点
,过点![]() 作抛物线
作抛物线![]() 的两切线,切点为
的两切线,切点为![]() .
.
(1)求两切点![]() 所在的直线方程;
所在的直线方程;
(2)椭圆![]() ,离心率为
,离心率为![]() ,(1)中直线AB与椭圆交于点P,Q,直线
,(1)中直线AB与椭圆交于点P,Q,直线![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,
,![]() ,若
,若![]() ,求椭圆的方程.
,求椭圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】地球的公转轨道可以看作是以太阳为一个焦点的椭圆,根据开普勒行星运动第二定律,可知太阳和地球的连线在相等的时间内扫过相等的面积,某同学结合物理和地理知识得到以下结论:①地球到太阳的距离取得最小值和最大值时,地球分别位于图中![]() 点和
点和![]() 点;②已知地球公转轨道的长半轴长约为
点;②已知地球公转轨道的长半轴长约为![]() 千米,短半轴长约为
千米,短半轴长约为![]() 千米,则该椭圆的离心率约为
千米,则该椭圆的离心率约为![]() .因此该椭圆近似于圆形:③已知我国每逢春分(
.因此该椭圆近似于圆形:③已知我国每逢春分(![]() 月
月![]() 日前后)和秋分(
日前后)和秋分(![]() 月
月![]() 日前后),地球会分别运行至图中
日前后),地球会分别运行至图中![]() 点和
点和![]() 点,则由此可知我国每年的夏半年(春分至秋分)比冬半年(当年秋分至次年春分)要少几天.以上结论正确的是( )
点,则由此可知我国每年的夏半年(春分至秋分)比冬半年(当年秋分至次年春分)要少几天.以上结论正确的是( )
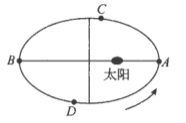
A.①B.①②C.②③D.①③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】斐波那契数列![]() 满足:
满足: ![]() .若将数列的每一项按照下图方法放进格子里,每一小格子的边长为1,记前
.若将数列的每一项按照下图方法放进格子里,每一小格子的边长为1,记前![]() 项所占的格子的面积之和为
项所占的格子的面积之和为![]() ,每段螺旋线与其所在的正方形所围成的扇形面积为
,每段螺旋线与其所在的正方形所围成的扇形面积为![]() ,则下列结论错误的是( )
,则下列结论错误的是( )
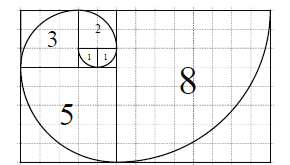
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从一批苹果中,随机抽取50个,其重量(单位:克)的频数分布表如下:

(1)根据频数分布表计算苹果的重量在![]() 的频率;
的频率;
(2)用分层抽样的方法从重量在![]() 和
和![]() 的苹果中共抽取4个,其中重量在
的苹果中共抽取4个,其中重量在![]() 的有几个?
的有几个?
(3)在(2)中抽出的4个苹果中,任取2个,写出所有可能的结果,并求重量在![]() 和
和![]() 中各有1个的概率.
中各有1个的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线C的参数方程为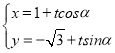 (a或t为参数).以O为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为ρ(cosθ
(a或t为参数).以O为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为ρ(cosθ![]() sinθ)=1.
sinθ)=1.
(1)当t为参数,α![]() 时,判断曲线C与直线l的位置关系;
时,判断曲线C与直线l的位置关系;
(2)当α为参数,t=2时,直线l与曲线C交于A,B两点,设P(1,0),求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(1)当![]() 时,求曲线
时,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)求函数![]() 在
在![]() 上的极值;
上的极值;
(3)设函数![]() ,若
,若![]() ,且对任意的实数
,且对任意的实数![]() ,不等式
,不等式![]() 恒成立(e是自然对数的底数),求实数a的取值范围.
恒成立(e是自然对数的底数),求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年4月8日零时正式解除离汉通道管控,这标志着封城76天的武汉打开城门了.在疫情防控常态下,武汉市有序复工复产复市,但是仍然不能麻痹大意,仍然要保持警惕,严密防范、慎终如始.为科学合理地做好小区管理工作,结合复工复产复市的实际需要,某小区物业提供了![]() ,
,![]() 两种小区管理方案,为了了解哪一种方案最为合理有效,物业随机调查了50名男业主和50名女业主,每位业主对
两种小区管理方案,为了了解哪一种方案最为合理有效,物业随机调查了50名男业主和50名女业主,每位业主对![]() ,
,![]() 两种小区管理方案进行了投票(只能投给一种方案),得到下面的列联表:
两种小区管理方案进行了投票(只能投给一种方案),得到下面的列联表:
|
| |
男业主 | 35 | 15 |
女业主 | 25 | 25 |
(1)分别估计![]() ,
,![]() 方案获得业主投票的概率;
方案获得业主投票的概率;
(2)判断能否有95%的把握认为投票选取管理方案与性别有关.
附: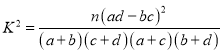 .
.
|
|
|
|
|
|
|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com