
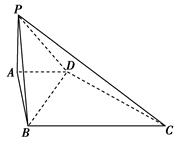
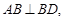 沿BD将
沿BD将 折起,使面
折起,使面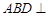 面
面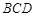 ,连结AC,则在四面体ABCD的四个面中,互相垂直的平面共有( )对
,连结AC,则在四面体ABCD的四个面中,互相垂直的平面共有( )对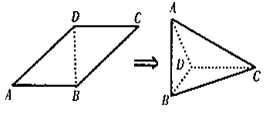
| A.1 | B.2 | C.3 | D.4 |
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 是
是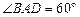 且
且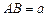 的菱形,
的菱形,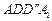 和
和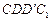 都是正方形。将两个正方形分别沿AD,CD折起,使
都是正方形。将两个正方形分别沿AD,CD折起,使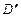 与
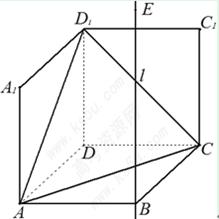
与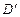 重合于点D1。设直线l过点B且垂直于菱形ABCD所在的平面,点E是直线l上的一个动点,且与点D1位于平面ABCD同侧,设
重合于点D1。设直线l过点B且垂直于菱形ABCD所在的平面,点E是直线l上的一个动点,且与点D1位于平面ABCD同侧,设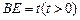 (图2)。
(图2)。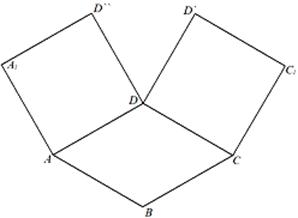
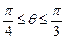 ,求
,求 的取值范围;
的取值范围;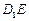 上是否存在点
上是否存在点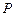 ,使平面
,使平面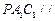 平面
平面 ,若存在,求出
,若存在,求出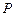 分
分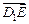 所成的比
所成的比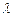 ;若不存在,请说明理由。
;若不存在,请说明理由。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
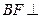 平面ACE。
平面ACE。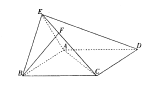
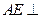 平面BCE;
平面BCE;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
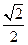 AB,∠ABC=60°,E为AB的中点.
AB,∠ABC=60°,E为AB的中点. 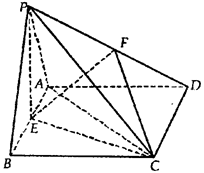
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 ,若
,若 ,且
,且 与
与 相交但不垂直,直线
相交但不垂直,直线 分别为
分别为 内的直线,则下列命题中:①任意
内的直线,则下列命题中:①任意 ;②任意
;②任意 ; ③存在
; ③存在 ; ④存在
; ④存在 ; ⑤任意
; ⑤任意 ; ⑥存在
; ⑥存在 。真命题的序号是_________ 。
。真命题的序号是_________ 。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com