
| A. | 2 | B. | $\frac{\sqrt{5}+1}{2}$ | C. | $\sqrt{3}$ | D. | $\sqrt{3}$+1 |
分析 求出双曲线右焦点关于直线y=$\sqrt{3}$x的对称点P的坐标,代入双曲线方程整理求得双曲线的离心率.
解答 解:双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1$的右焦点F(c,0),
设F(c,0)关于于直线y=$\sqrt{3}$x的对称点P(x0,y0),
则$\left\{\begin{array}{l}{\frac{{y}_{0}}{2}=\sqrt{3}•\frac{{x}_{0}+c}{2}}\\{\frac{{y}_{0}}{{x}_{0}-c}=-\frac{\sqrt{3}}{3}}\end{array}\right.$,解得:$\left\{\begin{array}{l}{{x}_{0}=-\frac{c}{2}}\\{{y}_{0}=\frac{\sqrt{3}}{2}c}\end{array}\right.$,即P($-\frac{c}{2},\frac{\sqrt{3}}{2}c$),
代入双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1$得:${e}^{2}=4-2\sqrt{3}$(舍),或${e}^{2}=4+2\sqrt{3}$.
∴e=$\sqrt{3}+1$.
故选:D.
点评 本题考查点关于直线的对称点的求法,考查了双曲线的简单几何性质,是基础的计算题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
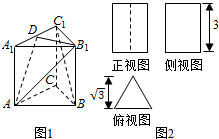 已知某几何体的直观图(图1)与它的三视图(图2),其中俯视图为正三角形,其它两个视图是矩形,已知D是棱A1C1的中点.
已知某几何体的直观图(图1)与它的三视图(图2),其中俯视图为正三角形,其它两个视图是矩形,已知D是棱A1C1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {2,4,5} | B. | {1,3,5} | C. | {2,4} | D. | {1,2,3,4,5} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 高效 | 非高效 | 统计 | |
| 新课堂模式 | 60 | 30 | 90 |
| 传统课堂模式 | 40 | 50 | 90 |
| 统计 | 100 | 80 | 180 |
| P(K2≧K0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| K0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.897 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
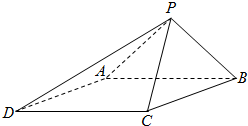 如图,已知四棱锥P-ABCD的底面为菱形,∠BCD=120°,AB=PC=2,AP=BP=$\sqrt{2}$.
如图,已知四棱锥P-ABCD的底面为菱形,∠BCD=120°,AB=PC=2,AP=BP=$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 甲校 | 乙校 | 丙校 | |
| 男生 | 97 | 90 | x |
| 女生 | 153 | y | z |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com